Combinations
1. Characterize combinations and combinations with repetition.
Solution:
a)
k-combinations from a set with n elements (without repetition)
k-combinations from a set of n elements (without repetition) is an unordered collection of k distinct elements taken from a given set.
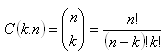
b)
k-combinations from a set with n elements (with repetition)
k-combinations from a set of n elements (without repetition) is an unordered collection of k not necessarily distinct elements taken from a given set.
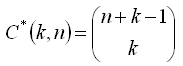
2. On the plane there are 6 different points (no 3 of them are lying on the same line). How many segments do you get by joining all the points?
Solution:
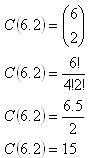
You get 15 different segments.
3.On a circle there are 9 points selected. How many triangles with edges in these points exist?
Solution:
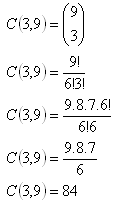
There are 84 such triangles.
4.a) Find out a formula for counting the number of diagonals in a convex n-gon!
b) How many diagonals has a 10-gon?
Solution:
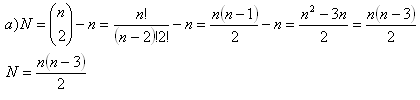
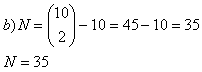
Convex 10-gon has 35 diagonals.
5. In how many ways you can choose 8 of 32 playing cards not considering their order?
Solution:
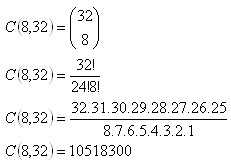
The playing cards can be chosen in 10 518 300 ways.
6.A teacher has prepared 20 arithmetics tasks and 30 geometry tasks. For a test he‘d like to use:
a) 3 arithmetics and 2 geometry tasks
b) 1 arithmetics and 2 geometry tasks
How many ways are there to build the test?
Solution:
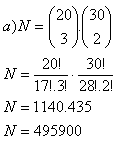
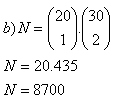
The teacher can choose from 495 900 tests or 8700 tests respectively.
7.On a graduation party the graduants pinged their glasses. There were 253 pings. How many graduants came to the party?
Solution:
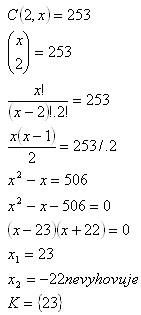
There were 23 graduants on the party.
8.If the number of elements would raise by 8, number of combinations with k=2 without repetition would raise 11 times. How many elements are there?
Solution:
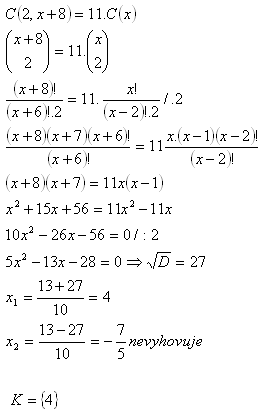
There are 4 elements.
9. For which x positive integer stands:
Solution:
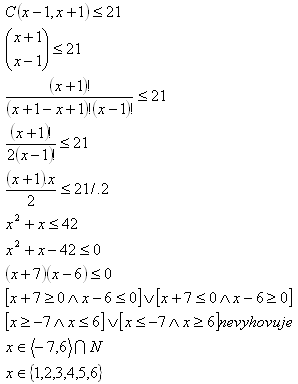
The inequality is valid for 1, 2, 3, 4, 5 and 6.
10.Two groups consist of 26 elements and 160 combinations without repetition for k=2 together. How many elements are in the first and how many in the second group?
Solution:
x – # of elements in the first group
y – # of elements in the second group
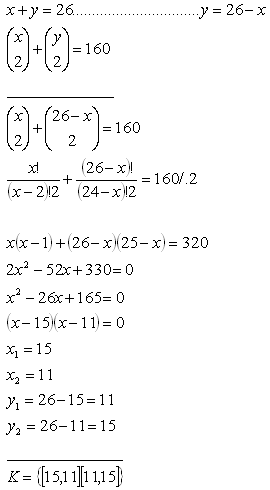
11. In the confectioners 5 different icecreams are sold. A father would like to buy 15 caps of icecream for his family. In how many ways can he buy the icecream?
Solution:
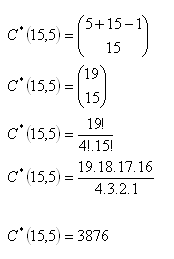
The father can buy the icecream in 3876 different ways.
12.From how many elements 15 combinations with repetition (k=2) can be made?
Solution:
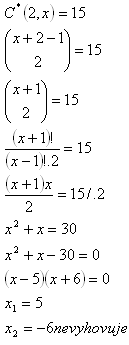
K = {5}
Combinations can be made from 5 elements.