Permutations
1. Define and characterize:
a) Permutations from n elements
b) Permutations from n elements with repetition
Solution:
Permutations
A pemutation is a sequence containing each element from a finite set of n elements once, and only once. Permutations of the same set differ just in the order of elements.
P(n) = n!
Permutations with repetition
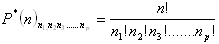
n1 – # of the same elements of the first cathegory
n2 - # of the same elements of the second cathegory
n3 - # of the same elements of the third cathegory
nj - # of the same elements of the j-th cathegory
Stands: n1+n2+n3+.........+nj = n
2. There are 3 elements a, b, c. Use them to make:
a) permutations (without repetition)
b) permutations with repetition, where „ a“ occures 2 times,“ b“ one time and „c“ one time
Solution:
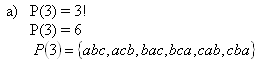
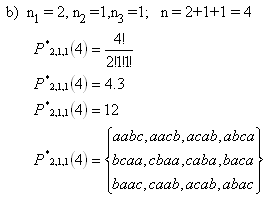
3.How many positive integers of 5 digits may be made from the ciphers 1,2,3,4,5, if:
a) Each cipher may be used just once?
b) How many of them will begin with 5?
c) How many of them will be even?
Solution:
a) P(5) = 5! = 5.4.3.2.1 = 120
b) P(4) = 4! = 4.3.2.1 =24
c)
ending with 2: P(4) = 4! =24
ending with 4: P(4) = 4! = 24
sum : S = 2.4! = 2.24 = 48
4.Eight students should be accomodated in two 3-bed and one 2-bed rooms. In how many ways can they be accomodated?
Solution:
Room #1: n1 = 3
Room #2: n2 = 3
Room #3: n3 = 2
n = 3 + 3 + 2 = 8
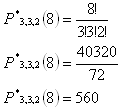
There are 560 ways of accomodating the students.
5.In how many ways can you throw a sum of 11 by 3 playing cubes?
Solution:
a) permutation of the triple 6,4,1 : P(3) = 3! = 6
b) permution of the triple 6,3,2 : P(3) = 3! = 6
c) permutation of the triple 5,5,1 : P2,1*(3) = 3
d) permutation of the triple 5,4,2 : P(3) = 3! = 6
e) permutation of the triple 5,3,3 : P*1,2(3) = 3
f) permutation of the triple 4,4,3 : P*2,1(3) = 3
Sum 6+6+3+6+3+3 = 27 ways.
6.There are 4 czech and 3 slovak books on the bookshelf. Czech books should be placed on the left side of the bookshelf and slovak books on the right side of the bookshelf. How many ways are there to arrange the books?
Solution:
Arranging czech books: P(4) = 4! =24
Arranging slovak books: P(3) = 3! = 6
N = P(4).P(3) = 24.6 = 144
The books may be arranged in 144 ways.
7. If the number of elements would raise by 2, the number of permutations without repetition would raise 42 times. How many elements are there?
Solution:
P(x + 2) = 42.P(x)
(x + 2)! = 42.x!
(x + 2)(x +1)x! = 42x!/: x!
(x + 2)(x + 1) = 42
x2 + 3x +2 - 42 = 0
x2 +3x – 40 = 0
(x – 5)(x + 8) = 0
x1 = 5
x2 = - 8 fails
K={5}
There are 5 elements.
8.Count all possible arrangements of 15 people on the foto.
a) How many fotos will be made?
b) How long would the photographing last if you need 10 seconds for one foto?
Solution:
a)
P(15) = 15! = 1,307.10
12
1,307.10
12 fotos will be made.
b)
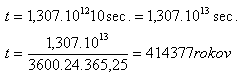
Photographing would last for 414 377 years.
9.A password of 6 digits is made of digits 926002.
How many possible passwords are there?
How long would it take to try all the possible passwords if trying one password takes 5 seconds?
Solution:
n
1 = 2, n
2 = 2, n
3 = 1, n
4 = 1, n = 6
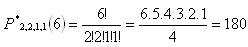
t = 180.5sec. = 900 sec. = 15 min
There are 180 possible passwords; trying all of them would take 15 minutes.
10. A student has to make 4 university entry exams. For passing each exam he gets either 2,3 or 4 points. He needs to reach at least 13 points to get to the university. In how many ways can he do the exams to be succesfull?
Solution:
He needs to get 13, 14, 15 or 16 points.
| 13 points: |
(3,3,3,4) |
P*3,1(4) = 4 |
| |
(4,4,3,2) |
P*2,1,1(4) = 12 |
| 14 points: |
(4,4,4,2) |
P*3,1(4) = 4 |
| |
(4,4,3,3) |
P*2,2(4) = 6 |
| 15 points: |
(4,4,4,3) |
P*3,1(4) = 4 |
| 16 points: |
(4,4,4,4) |
P*4(4) = 1 |
N = 4 + 12 + 4 + 6 + 4 + 1 = 31
There are 31 possible ways of reaching at least 13 points.