Astrofyzika
1.Jak se v astrofyzice určují vzdálenosti, hmotnost a jasnost hvězd?
Řešení:

2.Jak se získávají informace o hvězdách a vesmíru?
Charakterizujte:
- Wienův posuvný zákon
- Stefan–Boltzmannův zákon
- Zářivý tok
- Zářivý výkon
- Charakteristiky Slunce
- Rozpínání vesmíru
- Dopplerův zákon
- Hubbleův zákon
Řešení:

3.Vypočítejte, za jaký čas proletí světlo ve vakuu vzdálenost rovnající se
- a) průměru sluneční soustavy (s = 80 AU)
- b) průměru galaxie (s = 30 kpc)
Řešení:
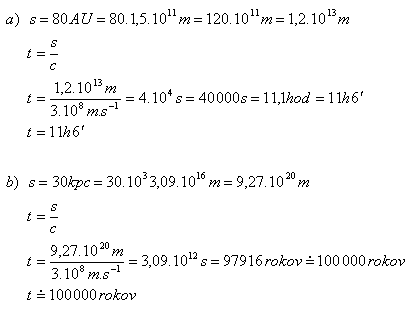
Světlo proletí průměr sluneční soustavy za 11 hodin, průměr galaxie za asi 100 000 let.
4.Vypočítejte střední hustotu látky ve Sluneční soustavě. Předpokládáme, že veškerou hmotnost soustavy vytváří Slunce (Mo = 2.1030kg) a že Sluneční soustava je koule s poloměrem R = 40 AU.
Pro zobrazení řešení se přihlaste.
5.Slunce obíhá kolem středu Galaxie rychlostí v = 250 km.s-1, přibližně po kružnici s poloměrem r = 10 kpc. Určete oběžnou dobu Slunce. Jak velkou gravitační silou je Slunce přitahováno ke středu Galaxie?
Pro zobrazení řešení se přihlaste.
6.Uvažujme o kulové hvězdokupě s hmotností MHK = 2.105Mo, která obíhá kolem středu Galaxie (MG = 1,4.1011Mo) po kružnici s poloměrem r = 12 kpc. Určete:
- a) sílu, kterou je hvězdokupa přitahována ke středu Galaxie
- b) dostředivé zrychlení hvězdokupy
- c) rychlost hvězdokupy vzhledem ke středu Galaxie
7.Odvoďte vzorec pro výpočet hmotnosti hvězdy (planety) pomocí její oběžnice.
Pro zobrazení řešení se přihlaste.
8.Vypočítejte hmotnost planety Mars pomocí měsíce Deimos, který obíhá kolem Marsu po kružnici s poloměrem r = 23,5.106m, s oběžným časem 1,26 dne (pozemského)
Pro zobrazení řešení se přihlaste.
9.Druhý Jupiterův měsíc Europa obíhá kolem Jupitera po kružnici s poloměrem r1 = 6,71.108m a s oběžnou dobou T = 3,88 dne. Vypočítejte, kolikrát je hmotnost Jupitera větší než hmotnost Země.
Pro zobrazení řešení se přihlaste.
10.Součet hmotností složek dvojhvězdy je 3,5Mo, složky obíhají kolem společného těžiště s periodou T = 320 let. Určete vzájemnou polohu složek kolmou na směr zorného paprsku, kterou bychom viděli pod úhlem π = 3,1//, a vzdálenost dvojhvězdy od Slunce.
Pro zobrazení řešení se přihlaste.
11.Zdánlivá hvězdná magnituda Slunce je -26,8m. Vypočítejte jeho absolutní magnitudu M.
Pro zobrazení řešení se přihlaste.
12.Do jaké vzdálenosti lze při měření vzdálenosti galaxií využít supernovu, která v nich zazářila, je-li její maximální absolutní magnituda –16M a máme dalekohled, kterým pozorujeme hvězdy do zdánlivé hvězdné magnitudy +22m?
Pro zobrazení řešení se přihlaste.
13.Jakou paralaxu π má hvězda, pokud rozdíl zdánlivé a absolutní hvězdné magnitudy je +8
Pro zobrazení řešení se přihlaste.
14.Jaká je vlnová délka, na kterou připadá maximum vyzařování, a intenzita vyzařování hvězdy, která má teplotu 30 000K?
Pro zobrazení řešení se přihlaste.
15.Červený obr má povrchovou teplotu 3500K, poloměr R = 36.Ro, hmotnost M = 3,6 Mo. Vypočítejte jeho průměrnou hustotu ρ a zářivý výkon L. (σ = 5,67.10-8W.m-2.K–4)
Pro zobrazení řešení se přihlaste.
16.Vypočítejte poloměr a průměrnou hustotu bílého trpaslíka, jehož hmotnost M = 2,35Mo, povrchová teplota T = 12 500K, zářivý výkon L = 0,0036 Lo. Ro = 6,96.108m, T0 = 5780K
Pro zobrazení řešení se přihlaste.
17.Jaký zářivý tok dopadá ze Slunce na plochu o obsahu S = 1m2 (zářivý výkon Slunce je L = 3,83.1026W)
- na Venuši (r = 0,72AU)
- na Jupiter (r = 5,2AU)
18.Hvězda má zdánlivou magnitudu m1 = 4. Jaká by byla zdánlivá magnituda m2 této hvězdy, kdyby byla ve dvojnásobné vzdálenosti od nás?
Pro zobrazení řešení se přihlaste.
19.Uvažujme o vzdálené galaxii, která se od naší Galaxie vzdaluje rychlostí v = 6000 km.s-1. Jakou vlnovou délku spektrální čáry vodíku změříme, je-li její původní vlnová délka 656,3 nm? V jaké vzdálenosti od nás se tato galaxie pravděpodobně nachází?
Pro zobrazení řešení se přihlaste.20.Určete dobu, po kterou se náš vesmír rozpíná. Určete čas, který uplynul od „velkého třesku“ do současnosti.
Pro zobrazení řešení se přihlaste.