Fyzikální význam derivace
1.V čem spočívá fyzikální význam derivace?
Řešení:
- Okamžitá rychlost v čase t0 je první derivací dráhy podle času:
v(t0) = s‘(t0).
- Okamžité zrychlení v čase t0 je první derivací rychlosti podle času:
a(t0) = v‘(t0)
Příklad:
Určete okamžitou rychlost a okamžité zrychlení pohybu v čase t, jehož dráha je dána vztahem: 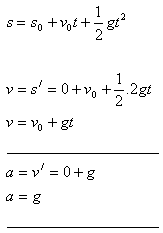
2.Kámen vyhozen z výšky h = 10m kolmo vzhůru má počáteční rychlost v0 = 20m.s-1. Jakou rychlost bude mít kámen v čase t = 1,5 s? Za jaký čas dosáhne maximální výšku? Jakou výšku dosáhne? (g = 10m.s-2)
Řešení:
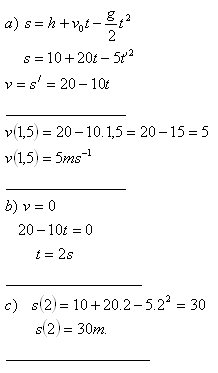
Rychlost kamene v čase t = 1,5s je v = 5ms-1. Maximální výši 30m dosáhne za 2 sekundy.
3.Těleso sjede po nakloněné rovině 50m dlouhé za 10s. Jaká je jeho konečná rychlost, pokud předpokládáme, že dráha je kvadratická funkce času a že počáteční rychlost je nulová.
Řešení:
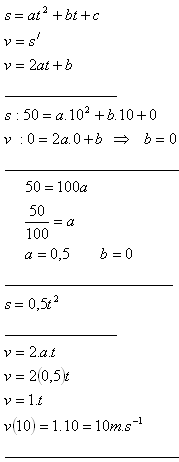
Konečná rychlost tělesa je v = 10m.s-1
4.Rychlík jedoucí rychlostí 90km.h-1 má zabrzdit tak, aby se rovnoměrně zpomaleným pohybem zastavil na vzdálenosti 1km. Po jakém čase zastaví?
5.Zjistěte jak rychle se mění výška s tlakem vzduchu.
Vzorec, který udává výšku nad zemským povrchem v závislosti na tlaku vzduchu. (p0 - je normální tlak vzduchu na hladině moře):
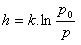
6.Určete rychlost změny napětí (p) vodních par od absolutní teploty (T), pokud platí:
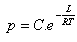
(C, L, R jsou konstanty)
7.Množství elektrického náboje Q, který prochází vodičem se mění s časem podle vztahu: Q = 3t2 +2t +2 . ( [Q] = C, [t] = sec )
8.V indukční cívce protéká proud i = 15.sin5 (3t), [i] = A, [t] = sec, [L = 0,03 H] Vypočtěte indukované elektromotorické napětí v čase t = 2π / 9 sec. podle vztahu:
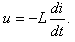
9.Těleso se pohybuje po přímce a pro jeho výchylku z rovnovážné polohy platí: y = 2cos2πt - 3sin2πt. Najděte jeho rychlost v čase t = 1s a největší výchylku z rovnovážné polohy. (y je v cm)
Pro zobrazení řešení se přihlaste.
10.Výkon baterie s elektromotorickým silou E a vnitřním odporem Ri je: P = EI - Ri.I2. Při jakém proudu dá baterie největší výkon? Určitě tento výkon.
Pro zobrazení řešení se přihlaste.
11.Pro výpočet dráhy harmonického pohybu platí s = A.sin (ω.t). Odvoďte vztah pro výpočet rychlosti a zrychlení harmonického pohybu.
Pro zobrazení řešení se přihlaste.
12.Závislost mezi množstvím a hmotností při některých chemických reakcích je dána rovnicí x = A.(1 – e–kt). (A, k jsou konstanty).
13.Setrvačník se otáčí, je kompenzován a začne se pohybovat podle rovnice:
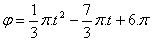
Napište rovnici úhlové rychlosti a zjistěte za jaký čas projde pohyb v rovnoměrný otáčivý s úhlovourychlostí
ω = π.
14.Pohyb pístu tam a zpět závisí na času podle rovnice s = –1,5t3 + 9t2 (cm). Vypočtěte maximální vzdálenost, kterou píst dosáhne za 4 sekundy. Určitě také rychlosti v0, v1,........v6.
Pro zobrazení řešení se přihlaste.
15.Při pohybu tělesa je dráha popsána rovnicí s = t2 + 3t - 5 (m) přičemž v čase t = 0 sec. byla jeho rychlost nulová. Určitě dráhu, rychlost a zrychlení v čase t = 5s. Určitě také jeho kinetickou energii, pokud jeho hmotnost je 8kg.
Pro zobrazení řešení se přihlaste.
16.Těleso se pohybuje po dráze s = t2 - t3 / 3 + 3t + 8 (m). Vypočtěte:
- a). za jaký čas zastaví
- b.) jaké bude jeho zrychlení v čase t = 0,5 s
- c.) jakou dráhu přejde těleso do zastavení
17.Množství elektrického náboje, který prochází vodičem se men podle vztahu Q = 2.te-t. Zjistěte čas, kdy se intenzita proudu bude rovnat nule.
Pro zobrazení řešení se přihlaste.
18.Ujistěte se, že daná funkce popisující průběh elektrického proudu Vybíjející se kondenzátoru, vyhovuje diferenciální rovnici:
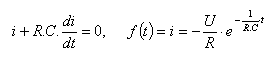
Pro zobrazení řešení se přihlaste.