Hydrostatika
1.Zopakujme si základní vlastnosti "ideální kapaliny".
Řešení:
Ideální kapalina je model kapaliny s těmito vlastnostmi:
- a) nemá viskozitu, je dokonale tekutá
- b) je kontinuum - neuvažujeme její částicovou strukturu
- c) je nestlačitelná
Stav kapaliny v určitém jejím bodě určuje tlak p:
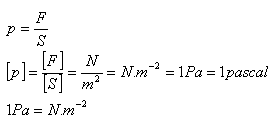
Tlak vyvolaný vnější silou - Pascalův zákon:
Tlak vyvolaný vnější silou působící na povrch kapaliny je ve všech místech kapaliny stejný. 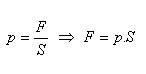
Tlak způsobený tíhou kapaliny - hydrostatický tlak
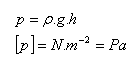
ρ – hustota kapaliny, g = 10m.s-2, h – hloubka, vzdálenost od povrchu
Hydraulický princip:
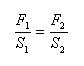
Archimedův zákon:
Těleso ponořené do kapaliny je nadlehčováno hydrostatickou vztlakovou silou, která se rovná tíze kapaliny tělesem vytlačené.
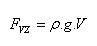
ρ – hustota kapaliny,
V – objem ponořené části tělesa
objem vytlačené kapaliny
2.Na píst s průměrem d = 20 cm, který je položen na povrchu kapaliny působíme silou F = 50 N. Jak velký tlak vyvolá síla v kapalině?
Řešení:
Rozbor:
d = 20 cm = 0,2 m, F = 50 N, p = ?
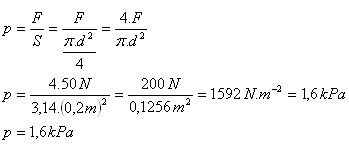
Síla vyvolá v kapalině tlak asi 1,6 kPa.
3.Vypočtěte tlak mořské vody (ρ = 1025 kg.m-3) na dno moře
- a.) v hloubce 3,6 km pod hladinou
- b.) v nejhlubší mořské propasti tzv.. Mariánském příkopu v Tichém oceánu (h = 11034 m)
Řešení:
- a.) p = ρ.g.h =1025 kg.m-3.10m.s-2.3600m =36 900 000 Pa = 36,9 MPa
- b.) p = ρ.g.h = 1025 kg.s-2.10 m.s-2.11034m = 113098500 Pa = 113,1 MPa
V hloubce 3,6 km je tlak mořské vody 36,9 MPa, na dně Mariánského příkopu je tlak mořské vody 113,1 MPa.
4.Lidé jsou během celého života zvyklí na tlak vzduchu kolem 1013 h Pa. Do jaké hloubky se mohou ponořit do mořské vody (ρ = 1025 kg.m-3) bez přístrojů?
Pro zobrazení řešení se přihlaste.
5.Do spojených nádob tvaru U byla nalita voda (ρ1 = 1000 kg.m-3) a rtuť. Voda v jednom rameni sahala do výšky h1 = 100 cm, rtuť v druhom rameni do výšky h2 = 7,35 cm. Určete hustotu rtuti ρ2
Pro zobrazení řešení se přihlaste.
6.Ve válcové nádobě s podstavou S = 100 cm2 jsou 2 kg rtuti (ρ1 = 13 600 kg.m-3) a 1 kg vody (ρ2 = 1000 kg.m-3). Určete hydrostatický tlak na dno nádoby!
Pro zobrazení řešení se přihlaste.
7.Vypočtěte tlakovou sílu působící na víčko zavařovacích lahve s průměrem 8 cm, pokud vnitřní tlak páry je 2,5 kPa a atmosférický tlak je 101325 Pa. (Předpokládáme, že vzduch uvnitř láhve je docela vyčerpaný).
Pro zobrazení řešení se přihlaste.
8.Turista naměřil na úpatí hory atmosférický tlak 1020 hPa, na vrcholu hory tlak 955 hPa. Jaký výškový rozdíl turista při výstupu na horu překonal? (ρvzduch = 1,3 kg.m-3)
Pro zobrazení řešení se přihlaste.
9.Malý hydraulický lis má průměr pístu 1,4 m, průměr pístu pumpy je 8 cm. Jak velká síla působí na píst lisu, jestliže na píst pumpy působí síla 4 N?
Pro zobrazení řešení se přihlaste.
10.Poloměr kruhové podstavy menšího pístu hydraulického lisu je 4 cm. Jaký poloměr musí mít kruhová podstava druhého většího pístu, jestliže silou 80 N třeba vyvolat tlakovou sílu 11 520 N.
Pro zobrazení řešení se přihlaste.
11.Norma udává, že v ponorce pro jednoho námořníka musí být průměrně 20 m3 prostoru. Kolik námořníků může pracovat v ponorce, pokud při ponoření do mořské vody (ρ = 1020 kg.m-3) působí na povrch ponorky vztlaková síla 15,3 MN.
Pro zobrazení řešení se přihlaste.
12.Dřevěný špalek plovoucí na vodě (ρ = 1000 kg.m-3) má ponořené dvě třetiny svého objemu. Jaká je hustota dřeva?
Pro zobrazení řešení se přihlaste.
13. Hustota morskej vody je 1030 kg.m-3, hustota ľadu je 915 kg.m-3. Koľko percent ľadovca vyčnieva nad voľnou hladinou mora?
Pro zobrazení řešení se přihlaste.
14.Jaký plošný obsah musí mít ledová kra (tvaru kvádru) tloušťky 30 cm, která unese člověka se zavazadly o celkové hmotnosti 96 kg.
Pro zobrazení řešení se přihlaste.15.Balón tvaru koule je naplněn vodíkem (ρ1 = 0,09 kg.m-3). Jaký musí být poloměr balónu, aby mohl nést zátěž 350 kg. Hustota vzduchu je ρ = 1,3 kg.m-3.
Pro zobrazení řešení se přihlaste.
16. Vysvětlete jak se vážením tělesa ve vzduchu av kapalině (ve vodě) lze zjistit hustota tělesa.
- ρ – hustota kapaliny
- ρ1- hledaná hustota tělesa
- Fg – tíha tělesa ve vzduchu (vážení tělesa ve vzduchu)
- F – tíha tělesa v kapalině (vážení tělesa v kapalině)
- FVZ – ρ.g.V (FVZ < Fg)
17.Vysvětlete, jak Archimédes (287 - 212 před nl) zjišťoval, zda královská koruna řeckého krále Hierona je z čistého zlata. (ρ1 = 19 290 kg.m-3). Jakou odpověď dal králi?
Pro zobrazení řešení se přihlaste.18.Zkumavka se stejným průřezem zatížená broky se ponoří do vody do hloubky 18 cm, ve zředěné kyselině sírové do hloubky 16 cm. Určitě hustotu zředěné kyseliny sírové.
Pro zobrazení řešení se přihlaste.
19. Oceľová koule (ρ1 = 7800 kg.m-3) je zavěšena na vlákně a ponořena do vody (ρ = 1000 kg.m-3). Objem koule je V = 1 dm3. Jakou silou je napínané vlákno?
Pro zobrazení řešení se přihlaste.
20.Kuličku zvážíme ve vzduchu i ve vodě. Získané hodnoty jsou Fg = 1,4 N, F = 0,84 N. Hustota vody: ρ = 1000 kg.m-3.
- a.) Z jakého materiálu je kulička?
- b.) Jaký je její poloměr
21.Jaká je hustota kamene s hmotností 12,6 kg, pokud na jeho vytažení z vody je potřebná síla, jejíž velikost je 81,2 N? Hustota vody 996,8 kg.m-3.
Pro zobrazení řešení se přihlaste.