Kuželosečky
1. Co víte o kuželosečkách:
Riešenie:
Kružnice je množina bodů roviny, které mají od pevného bodu roviny S stejnou vzdálenost r. S [m, n] je střed ar poloměr kružnice.
Elipsa je množina bodů roviny, jejichž součet vzdáleností od bodů F1,F2 roviny je roven 2a. Body F1[-e;0] ,F2[e;0] jsou ohniska, excentricita e2 = a2- b2, a – velká, b - malá poloos.
Hyperbola je množina bodů roviny, pro které absolutní hodnota rozdílu vzdiakeností od bodů F1,F2 roviny je roven 2a. Body F1[-e;0] , F2[e;0] jsou ohniska , excentricita e2 = a2 + b2. a – reální ,b – imaginární poloos. Rovnice asymtot hyperbboly: ( o || x ) : 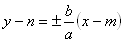
Parabola je množina bodů roviny, jejichž vzdálenost od bodu F roviny a od přímky d ležící v rovině je stejná. Bod F je ohnisko paraboly d - řídicí přímka. Bod F neleží na d. Hodnota p je parametr paraboly.
Vzájemnou polohu kuželosečky a přímky zjistíme řešením soustavy jejich rovnic, což vede na řešení kvadratické rovnice. Pokud D> 0 přímka je sečnica, jestliže D = 0 přímka je tečna, jestliže D <0 přímka je nesečnica.
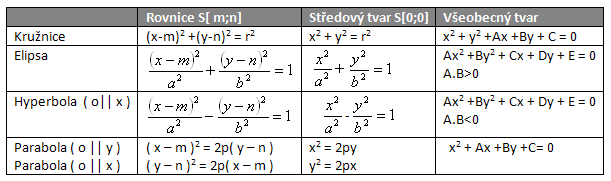
2.Napište rovnici kružnice, která má poloměr r = 8 a dotýká se obou souřadnicových os.
Řešení:
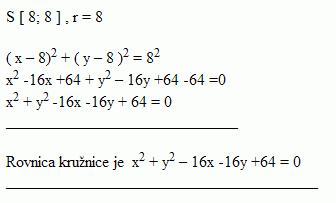
3.Napište rovnici kružnice, jejímž průměrem je úsečka AB, jestliže A [-1 ; 4 ], B [ 5 ; 6 ]
Řešení:
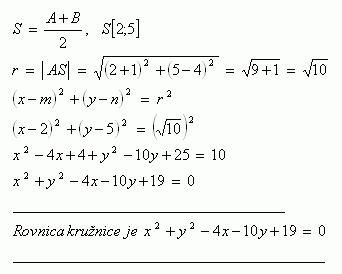
4. Dokažte, že rovnice k x2 + y2 +2x +4y +1 = 0 a k2 : x2 +y2-8x +6y + 9 = 0 představují kružnice. Napište rovnici přímky, která prochází středy těchto kružnic.
Pro zobrazení řešení se přihlaste.
5.Bodem A [4; 2] prochází kružnice, která se dotýká souřadnicových os. Napište rovnici této kružnice.
Pro zobrazení řešení se přihlaste.
6. Bod A [-4; 5] je vrcholem čtverce, jehož úhlopříčka leží na přímce p: [7x - y + 8 = 0]. Napište rovnici kružnice, která je mocnině popsána.
Pro zobrazení řešení se přihlaste.
7.Napište rovnici kružnice, jejíž střed S leží na přímce p: [x - y - 1 = 0] a která zároveň prochází body A [-1, -1] a B [0; 6]
Pro zobrazení řešení se přihlaste.
8.Napište rovnici kružnice, která prochází body K [2; -1] L [5; -2] M [10; 3]
Pro zobrazení řešení se přihlaste.
9.Vyšetřete vzájemnou polohu přímky p: [2x – y – 6 = 0] a kružnice k: [x2 + y2 – 4x -5y -1 = 0]
Pro zobrazení řešení se přihlaste.
10. Napište rovnici kružnice souměrné s kružnicí k1: ( x–1 )2 +(y–2)2 = 1 vzhledem na přímku p: x – y – 3 = 0
Pro zobrazení řešení se přihlaste.
11.Dva vrcholy kosočtverce jsou v ohniscích elipsy 9x2 + 25y2 - 225 = 0, další dva jsou ve vrcholech elipsy na její vedlejší osy. Vypočítejte obsah kosočtverce.
Pro zobrazení řešení se přihlaste.
12.Určete rovnici elipsy ve středovém tvaru S [0; 0], která prochází body A [8; 3] a [6; 4]
Pro zobrazení řešení se přihlaste.
13.Napište rovnici přímky, která prochází bodem A [1; 5] a středem elipsy 4x2 + 9y2 - 24x + 36y +36 = 0
Pro zobrazení řešení se přihlaste.
14.Do elipsy 2x2 + y2 – 4x + 4y – 108 = 0 je vepsán čtverec ABCD. Zjistěte jaký je jeho obvod a obsah.
Pro zobrazení řešení se přihlaste.
15. Zjistěte vzdálenost středu elipsy 4x2 + 9y2 -16x + 36y + 16 = 0 od přímky5x-12y+5 = 0
Pro zobrazení řešení se přihlaste.
16.Na elipse se středem S [3; 2], osou b = 4, excentricitou e = 3 najděte bod, jehož souřadnice y = 2
Pro zobrazení řešení se přihlaste.
17.Je dán trojúhelník Δ ABC se stranami | AB | = 6, | AC | = 7, | BC | = 3. Napište rovnici elipsy, která má ohniska v jeho dvou vrcholech a prochází třetím vrcholem trojúhelníku.
Pro zobrazení řešení se přihlaste.
18.Určitě a vyšetřete kuželosečky, která prochází body : K[0;0], L[8;0], M[0;6], N[8;6]. O[2;-2]
Pro zobrazení řešení se přihlaste.
19.Vypočítejte délku tětivy, kterou přímka 2x + y - 14 = 0 porážet na elipse 4x2 +y2 -100= 0
Pro zobrazení řešení se přihlaste.
20.Napište rovnici elipsy, kdy je dán bod M [3, -1], který je koncovým bodem malé poloosy b, ohniska leží na přímce p: y + 6 = 0. Pro excentricita elipsy platí:
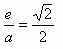
21.Určete střed a poloosy hyperboly 9x2 -16y2 -36x + 32y – 124 = 0. Určitě také rovnice asymptot hyperboly.
Pro zobrazení řešení se přihlaste.
22. Napište rovnici hyperboly, pokud pro její ohniska platí: F1 [-10; 2], F2 [16; 2]. Reálná os 2a = 24
Pro zobrazení řešení se přihlaste.
23. Napište rovnici přímky na níž leží os souměrnosti úsečky, která spojuje středy hyperbol x2 – y2 +6x -8y – 107 = 0, a 16x2 -9y2 -160x + 36y +220 = 0
Pro zobrazení řešení se přihlaste.
24.Dána je hyperbola 16x2 – 25y2 – 400 = 0. Napište:
- a) rovnice asymptot,
- b) úhel asymptot
Pro zobrazení řešení se přihlaste.
25.Napište osovou rovnici hyperboly, která prochází body:
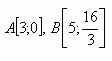
26.Dokažte, že součin vzdáleností libovolného bodu M hyperboly 2x2 – y2 – 2 = 0 od jejích asymptot je stálý a rovný 2: 3
Pro zobrazení řešení se přihlaste.
27.Najděte množinu všech bodů v rovině, které mají od bodu M [-5; 0] a od přímky p: 5x + 16 = 0 konstantní poměr vzdáleností rovný
5: 4
Pro zobrazení řešení se přihlaste.
28. Napište rovnici hyperboly, jejíž vrcholy jsou v ohniscích elipsy x2 + 2y2 – 18 = 0 a jejíž ohniska jsou ve vrcholech této elipsy
Pro zobrazení řešení se přihlaste.
29. Napište rovnici přímky, která prochází bodem M [5; 4] a vrcholem V paraboly y2- 6x +10y +31 = 0
Pro zobrazení řešení se přihlaste.
30. Dané jsou paraboly x2 - 8x - 3y +10 = 0 a x2 + 14x - 4y +61 = 0. Vypočítejte vzdálenost jejich vrcholů |V1V2|
Pro zobrazení řešení se přihlaste.
31.Napíšte rovnici paraboly (o||y) která prechochází body K[1;2], L[3;1], M[7;5].
Pro zobrazení řešení se přihlaste.
32.Na jaké čáře leží body v rovině, jejichž součet vzdáleností od osy xa od bodu B [8; 0] je stále stejný a rovný 24.
Pro zobrazení řešení se přihlaste.
33.Parabola má rovnici p: y2 = 8x. Vypočítejte souřadnice čtverce ABCD, jestliže A splývá s vrcholem paraboly, C leží na ose xa body B, D leží na parabole.
Pro zobrazení řešení se přihlaste.
34.Určitě stranu rovnostranného trojúhelníku Δ ABC vepsané do paraboly y2 = 5x
Pro zobrazení řešení se přihlaste.
35. Vypočítejte délku tětivy, kterou vytíná parabola y2 = 2x na elipse 4x2 + 9y2 – 400 = 0.
Pro zobrazení řešení se přihlaste.
36.Určete polohu bodů A.B, C, D v nichž elipsa x2 + 2y2 -18 = 0 přetíná hyperbolu x2 – y2 – 9 = 0.
Pro zobrazení řešení se přihlaste.
37. Na elipse najděte body, které mají od pravého ohniska (e> 0) vzdálenost r = 14. Rovnice elipsy:
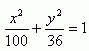
38.Vypočítejte obvod obdélníka ABCD, jehož vrcholy jsou průsečíky kružnice k: x2 + y2 = 50 a hyperboly h: x2 – y2 = 48.
Pro zobrazení řešení se přihlaste.