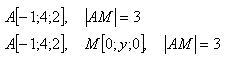Přímka v prostoru
1. Co víme o vlastnostech přímky v prostoru?
Řešení:

2.Napište parametrické vyjádření přímky, která prochází bodem A [2; 4; -3], rovnoběžně s přímkou BC, pokud B [3, 2, -1], C [7; 1; 9]. Zjistěte, který z bodů M [-1, 2, 0], N [6; 3; 7] leží na této přímce.
Řešení:

Na přímce p leží bod N [6;3;7]
3.Přímka p je rovnoběžná s přímkou AB jestliže A [4; -7; 2]. B [-1; 3; 6]. Určitě Yc a Zc tak, aby bod
C [2; Yc; Zc] ležel také na této přímce.
Řešení:
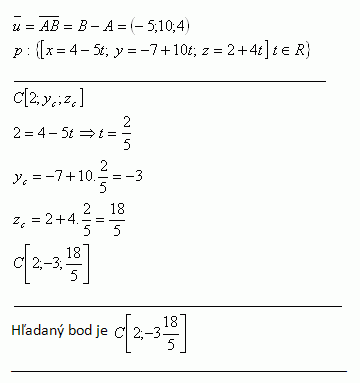
4.Dán trojúhelník Δ ABC vrcholy A [-2; 5; 4;], B [2, 3, -1], C [2; 7; -2]. Napište parametrické vyjádření stran trojúhelníku a = BC, b = AC,
c = AB
Pro zobrazení řešení se přihlaste.
5.Daný je bod M [3;2;-1] a parametrické vyjadrenie priamky p
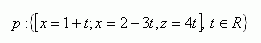
Napište :
- a) rovnice přímky q, která prochází bodem M rovnoběžně s p
- b) rovnice přímky q, která prochází bodem M kolmo k p
- c) rovnice přímky q, která je rovnoběžná s osou y
6.Zjistěte vzájemnou polohu přímek, jejichž parametrické vyjádření je:
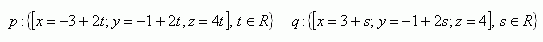
7.Dané jsou dvě přímky p a q. Zjistěte jejich vzájemnou polohu. Pokud se protínají zjistěte jejich průsečík a úhel mezi nimi.
Pro zobrazení řešení se přihlaste.
8.Zjistěte vzájemnou polohu přímek paq, jejich průsečík a úhel, který svírají. Vypočtěte také vzdálenost bodu M [5; -1; 4] od průsečíku přímek.
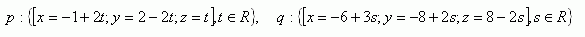
9.Rozhodněte, který z bodů A, B leží na přímce p, pokud platí:
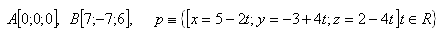
10.Napište parametrické vyjádření přímky, která prochází body A [3; -7; 2], B [5; -4; 1] a určete souřadnice x, z bodu C [x; 2; z] tak, aby ležel na přímce p..
Pro zobrazení řešení se přihlaste.11.Zjistěte vzájemnou polohu přímek paqv prostoru pokud platí:
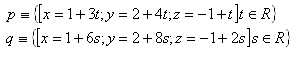
12.Určete vzájemnou polohu přímek paqv prostoru, pokud platí:
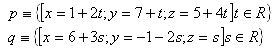
13.Určitě odchylku přímek paqv prostoru, pokud platí:
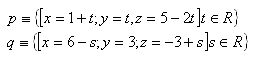
14.Určiete úhel mezi přímkami p a q v prostoru, pokud platí:
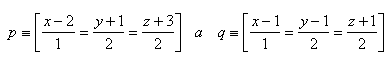
15.Dané jsou body A, B, C. Napište parametrické vyjádření přímky p, která prochází středy úseček AB a BC. Řešte pro body:
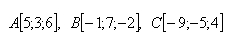
16.Vypočtěte vzdálenost bodu M od přímky p, jestliže platí:
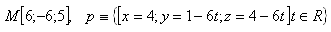
17.Dané jsou přímky p a q. Najděte vektor, který je kolmý na oba směrové vektory daných přímek.
Řešte pro přímky:
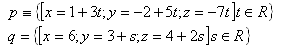
18.Dané jsou přímky p a q. Určitě "m" tak, aby přímky byly různoběžné. Určitě jejich průsečík.
Řešte pro přímky:
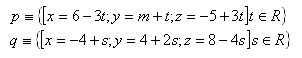
19.Vypočtěte vzdálenost bodu M od průsečíku přímek p a q. Řešte pro bod M [2, 3, -23] a přímky:
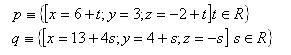
20.Daný je bod A [-1; 4; 2]. Na ose "y" určitě bod M, aby platilo | AM | = 3 Napište také parametrické vyjádření přímky AM.