Přímka v rovině
1. Vysvetlite rôzne druhy rovníc priamok v rovine.
- parametrický tvar
- všeobecný tvar
- smernicový tvar
- vzdialenosť bodu od priamky

2. Napíšte rovnicu priamky, ktorá prechádza bodmi A[2;7] a B[5;1] v tvare:
b) všeobecnom
c) smernicovom
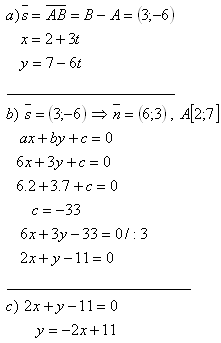
3. Napíšte rovnicu priamky, na ktorej leží os úsečky AB, ak A[1;5] a B[7;3].
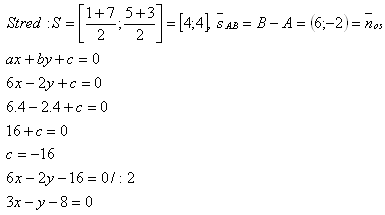
4. Napíšte rovnicu priamky, na ktorej leží výška vc v trojuholníku A[5;6], B[-2;4] a C[6;-1].
Pro zobrazení řešení se přihlaste.5. Daná je priamka (2–m)x + 3my + (2m-6) = 0.
a) priamka prechádzala počiatkom súradníc
b) priamka bola rovnobežná s osou x
c) priamka bola rovnobežná s osou y
6. Priamka je daná rovnicou p: 4x – 3y +6 = 0
b) preveďte ju na parametrický tvar
c) vypočítajte vzdialenosť bodu neležiaceho na priamke od tejto priamky
7. Napíšte rovnicu priamky, ktorá je rovnobežná s priamkou p: 5x +12y -1 = 0 a má od nej vzdialenosť d = 5 jednotiek.
Pro zobrazení řešení se přihlaste.8. Trojuholník má vrcholy A[-1;-5], B[9;-1] a C[1;7].
a) rovnicu strany c = AB
b) rovnicu ťažnice tc
c) rovnicu výšky na stranu c, vc
9. Napíšte rovnicu priamky, ktorá zviera s osou x uhol φ = 135° a prechádza bodom A[3;-1].
10. Svetelný lúč vychádza zo zdroja A[-1;-5], odráža sa na osi x ako od zrkadla a prechádza bodom B[9;-5].
11. Dané sú vrcholy trojuholníka A a B a priesečník výšok Q. Určite súradnice vrcholu trojuholníka C, ak platí
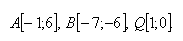
12. Na priamke p nájdite bod C, ktorý je rovnako vzdialený od bodov A,B.
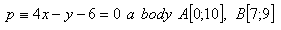
13.Vypočítajte dĺžku výšky va v trojuholníku ABC ak jeho strany majú rovnice
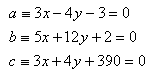
14. Protiľahlé strany štvorca ABCD ležia na rovnobežných priamkach
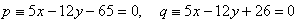
Vypočítajte obvod a obsah tohto štvorca.
15. Určite obvod a obsah pravouhlého trojuholníka, ktorý priamka 3x + 4y –12 = 0 vytína na súradnicových osiach.
Pro zobrazení řešení se přihlaste.16. Napíšte rovnicu priamky, ktorá je rovnobežná s priamkou 5x + 12y -1 =0 a má od nej vzdialenosť d = 5.
Pro zobrazení řešení se přihlaste.17. Vypočítajte vzdialenosť bodu A[2;-4] od priamky 3x + 4y = 0.
Pro zobrazení řešení se přihlaste.
18.Uhlopriečky kosoštvorca u1 = 4, u2 = 6 ležia na súradnicových osiach (u1 na osi x). Napíšte rovnice priamok na ktorých ležia strany kosoštvorca.
Pro zobrazení řešení se přihlaste.19. Určite rovnicu priamky, prechádzajúcej bodom [2;3] tak, aby úsek na osi x sa rovnal polovici úseku na osi y.
Pro zobrazení řešení se přihlaste.20. Dané sú body A[3;-2], B[1;4], C[-1;-3]. Určite bod D tak, aby priamka CD pretínala úsečku AB v jej strede S a aby platilo CD = 3.|CS|.
Pro zobrazení řešení se přihlaste.