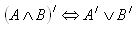Výroky
1.Charakterizujte základní vlastnosti výroků.
Řešení:
Výrok je každá oznamovací věta, o níž má smysl uvažovat zda je pravdivá nebo nepravdivá. Výroky označujeme: A, B, C, D, V, ... atd..
Výrok
- a) pravdivý - "platí" má pravdivostní hodnotu (1)
- b) nepravdivý - "neplatí" má pravdivostní hodnotu (0)
Negace výroku
Ke každému výroku A lze vytvořit výrok A ', který popírá (neguje) to, co tvrdí výrok A. Výrok A 'se nazývá negace výroku A. Negaci vytvoříme tak, že před výrok dáme předponu "ne ..", "není", nebo text "není pravda že ....".
| A | A‘ |
| (1) | (0) |
| (0) | (1) |
2.K daným výrokem vytvořte jejich negace. Určitě pravdivosti hodnoty původních a negován výroků.
A: Číslo 3 je prvočíslo (1)
B: Bratislava leží v Egyptě (0)
C: Prešovský kraj
D: Matematika je věda (1)
E: Číslo 22 je dělitelné 2 (1)
F: Dobrý den!
G: Existuje sněžný muž Yetti
H: Sinus 300 je - 2,1 (0)
I: Máš domácí úkol?
J: x2 -5x +6 = 0
K: Číslo 2574364 je dělitelné 4 (1)
L: Platí že (a + b)2 = a2 + b2 (0)
M: Obsah kruhu je S = π.r2 (1)
N: 42 sa rovná 18 (0)
O: Mám nové auto (1)
P: Není zde.
Řešení:
A ': Číslo 3 není prvočíslo (0
)B ': Bratislava neleží v Egyptě (1)
C: není výrok
D ': Matematika není věda (0)
E ': Číslo 22 není dělitelné 2 (0)
F: není výrok
G: nedá se rozhodnout
H ': Sinus 300 není -2,1 (1)
I: není výrok
J: není výrok
K ': Číslo 2574364 není dělitelné 4 (0)
L': Neplatí že ( a + b )2 = a2 + b2 (1)
M': Obsah kruhu není S = π.r2 (0)
N': Není pravda, že 42 se rovná 18 (1)
O': Nemám nové auto (0)
P : není výrok
3.Zopakujme si vlastnosti kvantifikovaného výroku.
Řešení:
Kvantifikovaný výrok je oznamovací věta, která udává určitý počet, nebo odhad počtu předmětů, osob atd.. se stejnou vlastností. V kvantifikovaných výroku se vyskytují slova: právě, nejvíce, každý, všichni, někteří, alespoň, žádný ... atd.., Které se nazývají kvantifikátor a číslovky.
Výrok "alespoň 5" znamená 5 a více.
Výrok "nejvíce 5" znamená 5 a méně
Pro symbolické zápisy kvantifikovaných výroků používáme:
- a) všeobecný kvantifikátor
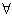- "pro každé (všechny) platí ....." - b) existenční kvantifikátor
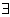- "existuje alespoň jedno ..., pro které platí ...."
Negace kvantifikovaného výroku
| Výrok | Negácia výroku |
| Každý ... je ... | Alespoň jeden ... není ... |
| Alespoň jeden ... je ... | Každý ... není ... |
| Alespoň n ... je ...(n>1) | Nejvíce (n-1)... je ... |
| Nejvíce n ... je ... (n>=1) | Alespoň (n+1)... je ... |
| Právě n ... je ... | Nejvíce (n-1) anebo alespoň (n+1) je... |
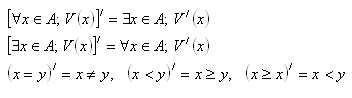
4. Negujte následující výroky:
A: Číslo 3 je kořenem rovnice x2 = 9 (1)
B : 23 -5 > 7 (0)
C: Úhlopříčky čtverce jsou na sebe kolmé (1)
D: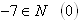 
E: Každá úloha má řešení (0)
F: Existuje alespoň jeden obdélník, který má kolmé úhlopříčky (0)
G: Existuje alespoň jeden pravoúhlý trojúhelník (1)
H: Tato kniha má nejvíce 50 stran (1)
I: Každá píseň má konec (1)
J: Na zasedání ZRPŠ bylo právě 20 rodičů (0)
K: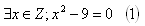 
L: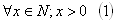 
5. Co víme o složených výrocích?
Pro zobrazení řešení se přihlaste.
6.Negujte následující výroky (SK):
A: Príde Peter a Mária
B: Prší a je mokro
C: Svieti slnko alebo fúka vietor
D: Ak sa nahneváme, budeme zlí
E: Ak príde Jozef, potom príde aj Eva
F: Mám dobrú náladu práve vtedy, keď prší
G: Každý lichobežník je rovnostranný
H: Existuje aspoň jedno prvočíslo, ktoré je párne
I: V triede 1.A aspoň 8 žiakov nosí okuliare
J: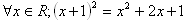 
7. Z daných výrokov A, B vytvorte:
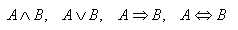
8.Dané jsou výroky P: prší, S: svítí Slunce, V: fouká vítr. Vytvořte z nich složené výroky
Pro zobrazení řešení se přihlaste.
9.Zjistěte pomocí tabulky pravdivostní hodnotu formule:
