Aritmetická posloupnost
1.Charakterizujte vlastnosti aritmetické posloupnosti.
Posloupnost (a2)∞n+1 je aritmetická právě tehdy, pokud existuje d є R, že pro všechny n є N platí
an+1 = an + d . Číslo d se nazývá diference aritmetické posloupnosti.
V aritmetické posloupnostii platí:
- an = a1 + (n-1)d
- ar = as + (r-s)d
- s = a1 + a2 + a3 + ... + an =
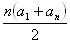
- Ak d > 0 je posloupnost rostoucí
- Ak d < 0 je posloupnost klesající
- Ak d = 0 je posloupnost konstantní
2.Zjistěte, zda je posloupnost aritmetická:
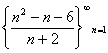
a1 = -2, a2 = -1, a3 = 0, a4 = 1, a5 = 2 atď.
Posloupnost je aritmetická s diferencí d = 1.
3.Napište prvních šest členů aritmetické posloupnosti pro kterou platí:
a5 – a2 – a3 = 2
a1 + a1 +3d +a1 +5d = 71
a1 + 4d – a1-d –a1 -2d = 2
3a1 + 8d = 71
-a1 + d =2/3
3a1 + 8d = 71
-3a1 + 3d = 6
a1 – d = -2
a1 = d - 2
a1 = 7 - 2
a1 = 5
11d = 77
d = 7
(a2)n-16 = 5;12;19;26;33;40
4.Napište prvních šest členů aritmetické posloupnosti pro kterou platí:
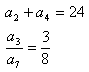
5.Osm čísel tvoří aritmetickou posloupnost. Určitě je, pokud víte, že součet prostředních členů je 41, součin krajních je 114.
Pro zobrazení řešení se přihlaste.6.Mezi kořeny kvadratické rovnice x2 - 16x +39 = 0 vložte čtyři čísla, aby spolu tvořily aritmetickou posloupnost.
Pro zobrazení řešení se přihlaste.7.Strany pravoúhlého trojúhelníku tvoří aritmetickou posloupnost. Delší odvěsna má 24 cm. Vypočítejte obvod trojúhelníku.
Pro zobrazení řešení se přihlaste.8.Zjistěte součet přirozených čísiel 1+2+3+4+5+6+7+.............+100.
Pro zobrazení řešení se přihlaste.9.Železné trubky jsou srovnané do osmi řad tak, že vrchní řada má 13 trubek a každý další o troubu víc. Kolik je všech trubek?
Pro zobrazení řešení se přihlaste.10.V trojúhelníku úhly tvoří aritmetickou posloupnost. Určete ostatní úhly, pokud nejmenší úhel má velikost 20°.
Pro zobrazení řešení se přihlaste.11.Hrany kvádru tvoří tři po sobě jdoucí členy aritmetické posloupnosti. Jaké jsou velké, pokud jejich součet je 24 cm a objem kvádru je 312 cm3?
Pro zobrazení řešení se přihlaste.12.Jak dlouho by padal kámen do dolu v Jižní Americe hluboké 2500 m, pokud víme, že v první vteřině proletí 4,904 ma za každou další o 9,808 m více?
Pro zobrazení řešení se přihlaste.