Krychle, kvádr, hranol a válec

1.Uveďte základní vztahy pro výpočet objemu a povrchu:

Řešení:

Krychle

a – hrana krychle

objem V = a³

obsah S = 6a²



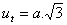
Kvádr

a, b, c – hrany kvádru

objem V = a.b.c

obsah S = 2(ab+ac+bc)



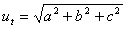
Hranol

S_p – obsah podstavy
Q – obsah pláště
v – výška hranolu

objem V = S_p.v

obsah S = 2S_p + Q

Válec

r – poloměr podstavy
v – výška valce

objem V = π.r².v

obsah S = 2πr(r+v)

Q = 2πrv

2. Dvě krabice tvaru krychle s hranami a = 70 cm, b = 90 cm je třeba nahradit jednou krabicí tvaru kostky.

Řešení:



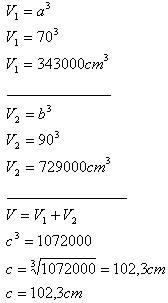
Hrana náhradní kostky bude c = 102,3 cm.

3. Hrana druhé kostky je o 2 cm větší, než hrana první kostky. Rozdíl objemů kostek je 728 cm³.

Řešení:

Hrana první kostky: x
Hrana druhé kostky: x + 2



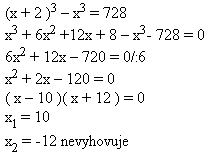
Hrana první kostky je 10 cm, druhé 12 cm.

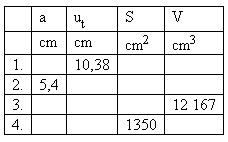
4. Daná je krychle o hraně a. Známé hodnoty jsou v tabulce.

Doplňte tabulku!

5. Hrany dvou kostek se liší o 22 cm. Jejich povrchy se liší o 19272 cm².

6. Kvádr má rozměry a = 4 cm, b = 3 cm, c = 5 cm.

7. Povrch kvádru je S = 376 cm². Pro jeho hrany platí a:b:c = 3:4:5.

8. Ve vodojemy tvaru kvádru je 1500 hl vody, výška vody je 2,5 m.

9. Vypočítejte objem kvádru, pokud jeho podstava má S₁ = 272 cm² a bočné stěny S₂ = 240 cm², S₃ = 255 cm².

10. Jakou hmotnost má železná tyč (ρ = 7800 kg.m^-3) 1,5 metrů dlouhá, jejímž průřezem je čtverec se stranou a = 45 mm?

11. Podstava kolmého trojboké hranolu je pravoúhlý trojúhelník s odvěsnami a = 9 cm, b = 12 cm. Výška hranolu je dvojnásobek přepony pravoúhlé podstavy hranolu.

12. Kolik zeminy je třeba přemístit při výkopu přímého 170 m dlouhé příkopy, jejíž průřez je rovnoramenný lichoběžník se základnami a = 150 cm, c = 80 cm a výškou v = 83 cm?

13. Vypočtete objem a povrch hranolu, jehož podstava je kosočtverec s úhlopříčkami u₁ = 12 cm, u₂ = 16 cm. Výška hranolu se rovná dvojnásobku podstavovej hrany.

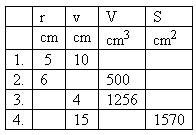
14. V tabulce jsou veličiny charakterizující různé válce.

Doplňte tabulku!

15. Plášť rotačního válce rozvinutý do roviny je čtverec s obsahem a² = 81 cm².

16. Rovnostranný válec (v = 2r) má objem V = 250 cm³.

17. Hliníkový drát (ρ = 2,7 g.cm^-3) s průměrem d = 3 mm má celkovou hmotnost m = 1,909 kg.

18. Vnější obvod mosazné trubky (ρ = 8,5 g.cm^-3) je 31,4 cm. Její hmotnost je 3,14 kg a délka je 60 cm.

Zaregistruj se a odemkni všechny řešení!

Na priklady.eu najdeš spoustu cvičení, vzorových řešení a užitečných materiálů.
Registrovaní uživatelé vidí celý obsah – bez omezení!
Stačí se přihlásit a začít se učit efektivně.

Zaregistruj se nyní a začni s učením!

Máš už vytvořený účet? Přihlas se