Kvadratura
1.Vysvětlete pojem "kvadratura"
Řešení:
Kvadratura je výpočet obsahu rovinného útvaru, který je ohraničen osou x, dvěma rovnoběžkami s osou yv bodech x1 = a, x2 = b a čárou (přímkou nebo křivkou), která má rovnici y = f (x).
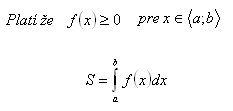
2.Pomocí určitého integrálu odvoďte vzorec pro výpočet obsahu
- a) čtverce
- b) obdélníka
Řešení:
a) Čtverec
Čtverec je ohraničen osou x, přímkou y = aa přímkami rovnoběžnými s osou yv bodech a = 0, b = a.
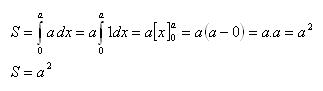
b) Obdélník
Obdélník je ohraničen osou x, přímkou y = ba přímkami rovnoběžnými s osou yv bodech a = 0, b = a.
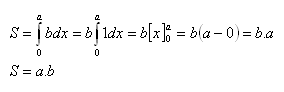
3.Pomocí určitého integrálu odvoďte vzorec pro výpočet obsahu
- a) rovnoramenného trojúhelníku
- b) rovnoramenného lichoběžníku
Řešení:
a) Rovnoramenného trojúhelník
Rovnoramenný trojúhelník má základnu a, výšku v. Nechť S1 je poloviční obsah tohoto trojúhelníku, který je ohraničen osou x, přímkami rovnoběžnými s osou yv bodech a = 0, b = v a přímkou
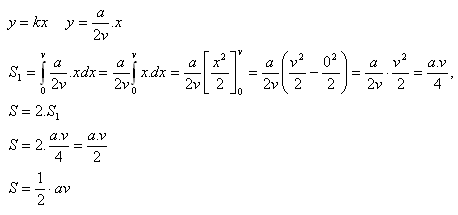
b) Rovnoramenného lichoběžník
Rovnoramenný lichoběžník má horní základnu a, dolní ba výšku v. Nechť S1 je poloviční obsah tohoto lichoběžníku, který je ohraničen osou x, přímkami rovnoběžnými s osou yv bodech a = 0, b = v a přímkou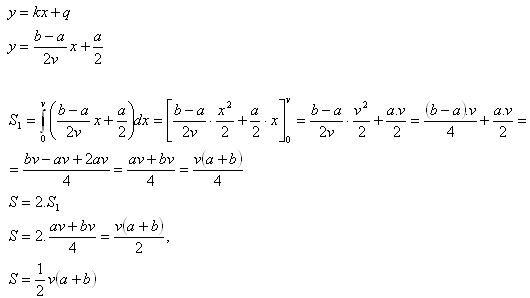
4.Vypočítejte obsah útvaru ohraničeného parabolou y = x2 + 1 a přímkou y = 5.
Pro zobrazení řešení se přihlaste.
5.Pomocí určitého integrálu vypočítejte obsah rovinného útvaru ohraničeného parabolami
y = 6 – 4x + x2 a y = –3 + 8x –2x2.
Pro zobrazení řešení se přihlaste.
6. Odvoďte vzorec pro výpočet obsahu kruhu o poloměru r.
Pro zobrazení řešení se přihlaste.
7.Odvoďte vzorec pro obsah elipsy, jejíž poloosy jsou "a" a "b".
Pro zobrazení řešení se přihlaste.