Die physikalische Bedeutung der Ableitung
1. Was ist die physikalische Bedeutung der Ableitung?
Lösung:
- Die momentane Geschwindigkeit zum Zeitpunkt t0 ist die erste Ableitung des Weges nach der Zeit:
v(t0) = s‘(t0).
- Die momentane Beschleunigung zum Zeitpunkt t0 ist die erste Ableitung der Geschwindigkeit nach der Zeit:
a(t0) = v‘(t0)
Beispiel:
Bestimme die momentane Geschwindigkeit und die momentane Beschleunigung einer Bewegung zum Zeitpunkt t, deren Weg durch die Beziehung gegeben ist: 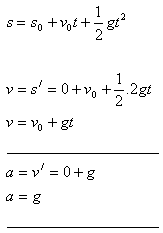
2.Ein Stein wird von einer Höhe h = 10 m mit einer Anfangsgeschwindigkeit v0 = 20 m·s-1 senkrecht nach oben geworfen. Welche Geschwindigkeit hat der Stein zum Zeitpunkt t = 1,5 s? Nach welcher Zeit erreicht er seine maximale Höhe? Welche Höhe erreicht er? (g = 10 m·s-2)
Lösung:
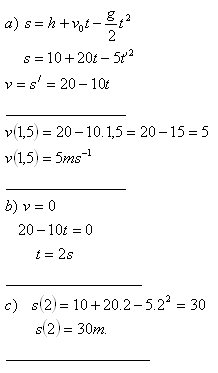
Die Geschwindigkeit des Steins zum Zeitpunkt t = 1,5 s ist v = 5 m·s-1. Er erreicht nach 2 Sekunden die maximale Höhe von 30 m.
3.Ein Körper gleitet eine geneigte Ebene der Länge 50 m in 10 s hinunter. Wie groß ist seine Endgeschwindigkeit, wenn der Weg eine quadratische Funktion der Zeit ist und die Anfangsgeschwindigkeit null ist?
Lösung:
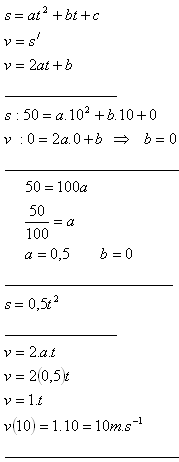
Die Endgeschwindigkeit des Körpers ist v = 10 m·s-1.
4.Ein Schnellzug fährt mit 90 km·h-1 und muss gleichmäßig bremsen, sodass er auf einer Strecke von 1 km zum Stillstand kommt. Nach welcher Zeit bleibt er stehen?
5.Bestimme, wie schnell sich die Höhe mit dem Luftdruck ändert.
Die Formel, die die Höhe über der Erdoberfläche als Funktion des Luftdrucks angibt (p0 ist der Standardluftdruck auf Meereshöhe):
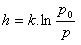
6.Bestimme die Änderungsrate des Dampfdrucks (p) in Bezug auf die absolute Temperatur (T), wenn gilt:
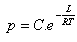
(C, L, R sind Konstanten)
7.Die durch einen Leiter fließende elektrische Ladungsmenge Q ändert sich mit der Zeit nach Q = 3t2 + 2t + 2. ([Q] = C, [t] = s)
8.In einer Induktionsspule ist der Strom i = 15·sin5(3t), [i] = A, [t] = s, [L] = 0,03 H. Berechne die induzierte elektromotorische Kraft zum Zeitpunkt t = 2π/9 s nach der Formel:
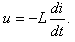
9.Ein Körper bewegt sich entlang einer Geraden und seine Auslenkung aus der Gleichgewichtslage ist gegeben durch: y = 2cos2πt - 3sin2πt. Bestimme seine Geschwindigkeit zum Zeitpunkt t = 1 s und die maximale Auslenkung aus der Gleichgewichtslage. (y in cm)
Bitte melden Sie sich an, um die Lösung anzuzeigen.
10.Die Leistung einer Batterie mit der elektromotorischen Kraft E und dem Innenwiderstand Ri ist: P = E·I – Ri·I2. Bei welcher Stromstärke liefert die Batterie die maximale Leistung? Bestimme diese Leistung.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
11.Für die Auslenkung einer harmonischen Bewegung gilt s = A·sin(ω·t). Leite die Formeln für die Geschwindigkeit und Beschleunigung der harmonischen Bewegung her.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
12.Die Beziehung zwischen Stoffmenge und Masse in einigen chemischen Reaktionen ist gegeben durch
x = A·(1 – e–kt). (A, k sind Konstanten).
13.Ein Schwungrad rotiert, wird abgebremst und seine Bewegung ist durch die Gleichung beschrieben
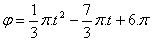
Schreibe die Gleichung für die Winkelgeschwindigkeit und bestimme, nach welcher Zeit die Bewegung zu einer gleichförmigen Rotation mit der Winkelgeschwindigkeit ω = π wird.
14.Ein Kolben führt eine Hin- und Herbewegung aus, die durch s = –1,5 t3 + 9 t2 (cm) beschrieben wird. Berechne die maximale Entfernung, die der Kolben in 4 Sekunden erreicht. Bestimme außerdem die Geschwindigkeiten v0, v1, ... v6.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
15.Für einen sich bewegenden Körper ist der Weg durch s = t2 + 3t – 5 (m) gegeben, und zum Zeitpunkt t = 0 war seine Geschwindigkeit null. Bestimme Weg, Geschwindigkeit und Beschleunigung zum Zeitpunkt t = 5 s. Bestimme außerdem seine kinetische Energie, wenn seine Masse 8 kg beträgt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
16.Ein Körper bewegt sich auf der Bahn s = t2 – t3/3 + 3t + 8 (m). Berechne
- a.) nach welcher Zeit er zum Stillstand kommt
- b.) wie groß seine Beschleunigung zum Zeitpunkt t = 0,5 s ist
- c.) welche Strecke der Körper bis zum Stillstand zurücklegt
17.Die durch einen Leiter fließende elektrische Ladungsmenge ändert sich nach Q = 2·t·e–t. Bestimme den Zeitpunkt, zu dem die Stromstärke null ist.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
18.Überprüfe, dass die gegebene Funktion, die den Strom eines entladenden Kondensators beschreibt, die Differentialgleichung erfüllt:
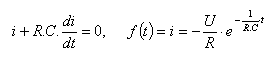
Bitte melden Sie sich an, um die Lösung anzuzeigen.