Die Menge

1. Erkläre den Begriff einer Menge und die Mengenoperationen.

Lösung:

Eine Menge ist eine Zusammenfassung von Gegenständen (Objekten, Personen, Zahlen usw.),
die wir Elemente nennen. Eine Menge ist festgelegt, wenn wir für jedes Objekt entscheiden können, ob es zur Menge gehört oder nicht.
Mengen bezeichnen wir mit Großbuchstaben A, B, M, Q, R…
Elemente einer Menge bezeichnen wir mit Kleinbuchstaben a, b, x, y, …

A={2; −5; 73; x},−5∈A,y∉AA = \{2;\,-5;\,\tfrac{7}{3};\,x\},\quad -5 \in A,\quad y \notin A

Darstellung einer Menge

a) Durch Aufzählung aller Elemente

A={1,2,3,4,5,6,7}A = \{1, 2, 3, 4, 5, 6, 7\}

b) Durch Angabe einer gemeinsamen Eigenschaft der Elemente, die zur Menge gehören

A={x∈N; x≤7}A = \{x \in \mathbb{N};\ x \leq 7\}

Mengenoperationen

Komplement der Menge A ist die Menge aller Elemente von M, die nicht zur Menge A gehören.

A′={x∈M; x∉A}A' = \{x \in M;\ x \notin A\}

Schnittmenge (Durchschnitt) zweier Mengen A und B ist die Menge aller Elemente von M, die zugleich zu A und zu B gehören.

A∩B={x∈M; x∈A und x∈B}A \cap B = \{x \in M;\ x \in A \ \text{and} \ x \in B\}

Vereinigung zweier Mengen A und B ist die Menge aller Elemente von M, die zu A oder zu B gehören (sie können auch zu beiden gehören).

A∪B={x∈M; x∈A oder x∈B}A \cup B = \{x \in M;\ x \in A \ \text{or} \ x \in B\}

Differenz zweier Mengen A – B ist die Menge aller Elemente von M, die zu A gehören und nicht zu B.

A−B={x∈M; x∈A und x∉B}A - B = \{x \in M;\ x \in A \ \text{and} \ x \notin B\}

Teilmenge:
Die Menge B ist eine Teilmenge der Menge A, wenn alle Elemente von B auch zu A gehören.

B⊆A ⟺ (∀x∈M; x∈B⇒x∈A)B \subseteq A \iff (\forall x \in M;\ x \in B \Rightarrow x \in A

2. Liste alle Elemente der folgenden Mengen auf:

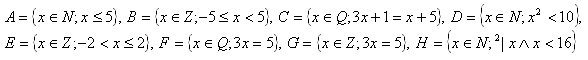
Mengen – Aufgabe 2

Lösung:

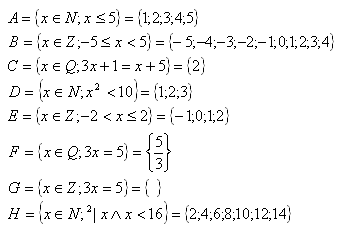
Mengen – Lösung zu Aufgabe 2

3. Es sind folgende Mengen gegeben:

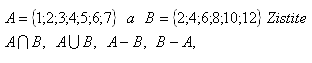
Mengen – Aufgabe 3

Lösung:

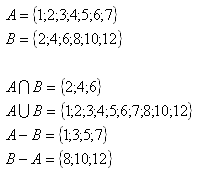
Mengen – Lösung zu Aufgabe 3

4. Es sind folgende Mengen gegeben:

Mengen – Aufgabe 4
Bitte melden Sie sich an, um die Lösung anzuzeigen.

5. Es sind folgende Mengen gegeben:

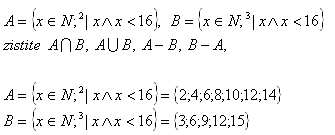
Mengen – Aufgabe 5
Bitte melden Sie sich an, um die Lösung anzuzeigen.

6. Stelle die gegebenen Mengen als Intervalle dar:

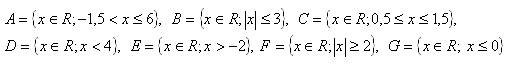
Mengen – Aufgabe 6
Bitte melden Sie sich an, um die Lösung anzuzeigen.

7. Es sind folgende Intervalle gegeben:

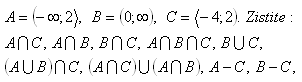
Mengen – Aufgabe 7
Bitte melden Sie sich an, um die Lösung anzuzeigen.

8. Erkläre, wie man die Anzahl der Elemente in endlichen Mengen berechnet.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

9. Auf einem Empfang der Botschaft spricht jeder mindestens eine Fremdsprache. 15 Personen sprechen Englisch, 12 sprechen Deutsch und 7 sprechen beide Sprachen. Wie viele Personen sind insgesamt anwesend, wenn niemand andere Sprachen spricht?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

10.Von 35 Schülern abonnieren 8 die Tageszeitung SME, 10 die Pravda und 21 Schüler abonnieren keine dieser Zeitungen. Wie viele Schüler abonnieren beide Zeitungen?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

11.An einem Tag reparierte die Autowerkstatt 24 Bremsprobleme und 36 Motorprobleme an 46 Autos. Wie viele Autos hatten nur Bremsprobleme und wie viele nur Motorprobleme?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

12.Eine Umfrage zu Lesegewohnheiten ergab: 60 % der Schüler lesen Zeitschrift A, 50 % Zeitschrift B, 50 % Zeitschrift C, 30 % sowohl A als auch B, 20 % sowohl B als auch C, 30 % sowohl A als auch C und 10 % alle drei Zeitschriften. Wie viel Prozent der Schüler lesen genau zwei Zeitschriften und wie viel Prozent lesen keine dieser Zeitschriften?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

13.Stelle die Mengen mit Hilfe von Venn-Diagrammen dar:

Mengen – Aufgabe 13
Bitte melden Sie sich an, um die Lösung anzuzeigen.