Diophantische Gleichungen
1. Löse die Gleichungen:
Lösung:
Der griechische Mathematiker DIOPHANTUS (etwa 250 v. Chr.) beschäftigte sich mit dem Lösen von Gleichungen der Form ax + by = c, wobei nur ganzzahlige Lösungen akzeptiert wurden. Solche Gleichungen nennt man „diophantische Gleichungen“.
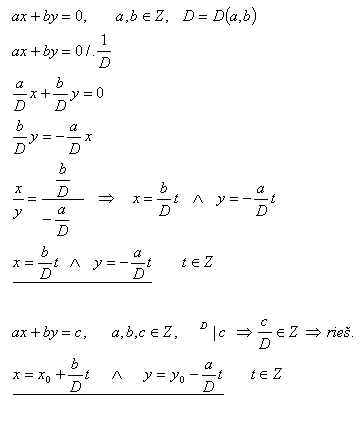
2.In der Menge Z löse die Gleichung:
Lösung:
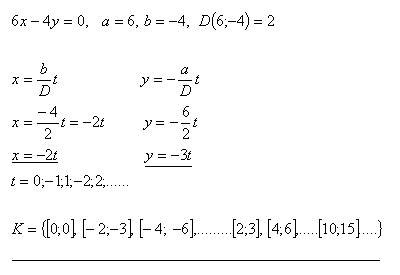
3.In der Menge Z löse die Gleichung:
Lösung:
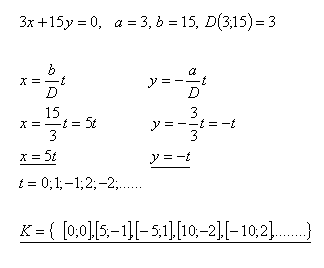
4.Finde heraus, welche der folgenden Gleichungen in der Menge Z lösbar sind:
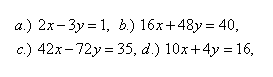
5.In der Menge Z löse die Gleichung:
6.In der Menge Z löse die Gleichung:
7.Welche ganzzahligen Abmessungen kann ein Rechteck haben, wenn sein Umfang 24 cm beträgt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.8.Auf welche Arten kann man die Summe von 21 Euro bezahlen, wenn man nur 2-Euro- und 5-Euro-Münzen hat?
Bitte melden Sie sich an, um die Lösung anzuzeigen.9.Bestimme, auf wie viele Arten 22 Liter Wein in 2-Liter- und 3-Liter-Gefäße abgefüllt werden können.
Bitte melden Sie sich an, um die Lösung anzuzeigen.10.Ein 50 cm langes Band soll in Stücke von 6 cm und 4 cm Länge geschnitten werden. Auf wie viele Arten kann dies geschehen?
Bitte melden Sie sich an, um die Lösung anzuzeigen.11.Bestimme alle gleichschenkligen Dreiecke, deren Seitenlängen ganze Zahlen sind und deren Umfang 40 cm beträgt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.