Funktionsmerkmale
1. Was erinnerst du dich über die Eigenschaften von Funktionen?
Lösung:
Eine Funktion f einer reellen Variablen x ist eine Vorschrift, die jedem x ∈ R höchstens ein y ∈ R zuordnet, so dass
y = f(x)
Die Definitionsmenge der Funktion D ist die Menge aller x ∈ R, für die es genau ein y ∈ R gibt, so dass
y = f(x).
Die Wertemenge der Funktion H ist die Menge aller y ∈ R, für die es mindestens ein x ∈ R gibt, so dass
y = f(x).
, dann ist die Funktion streng monoton steigend
, dann ist die Funktion streng monoton fallend
, dann ist die Funktion monoton fallend
, dann ist die Funktion monoton steigend
, dann ist die Funktion injektiv
Wenn es ein gibt, so dass , dann ist die Funktion nach oben beschränkt
Wenn es ein R gibt, so dass , dann ist die Funktion nach unten beschränkt
Wenn die Funktion nach oben und nach unten beschränkt ist, ist sie beschränkt
Wenn , dann ist die Funktion periodisch ( Periode)
Wenn , dann ist die Funktion gerade
Wenn , dann ist die Funktion ungerade
Eine Funktion besitzt eine Umkehrfunktion . Es gilt:
Zwei Funktionen sind gleich: f(x) = g(x), wenn: D(f) = D(g)
f(x) = g(x)
Welche der folgenden Graphen stellen Funktionen dar? 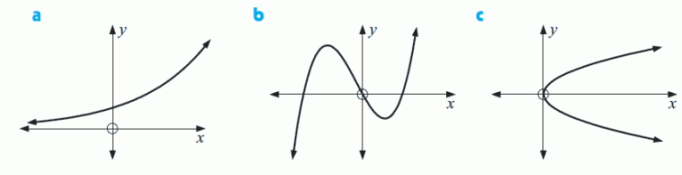
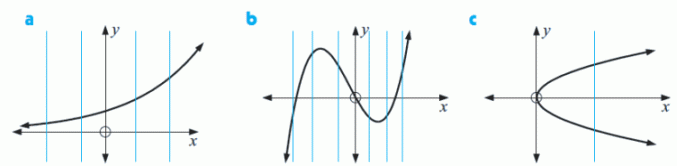
Funktion Funktion Keine Funktion
2.Bestimmen Sie, ob die folgenden Ausdrücke Funktionen sind:
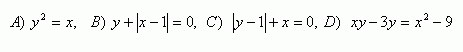
Lösung:
A)
, Wenn , dann oder
Der Ausdruck ist keine Funktion.
B)
oder
und
,
Der Ausdruck stellt zwei Funktionen dar.
Für :
Für :
C)
oder
Wenn , dann und
Der Ausdruck ist keine Funktion.
D)
, falls , dann
Der Ausdruck ist eine Funktion.
3.Entscheiden Sie, ob die folgenden Funktionen gleich sind:
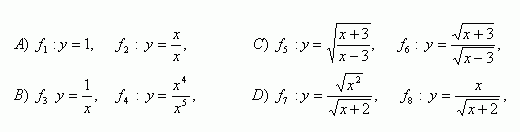
Lösung:
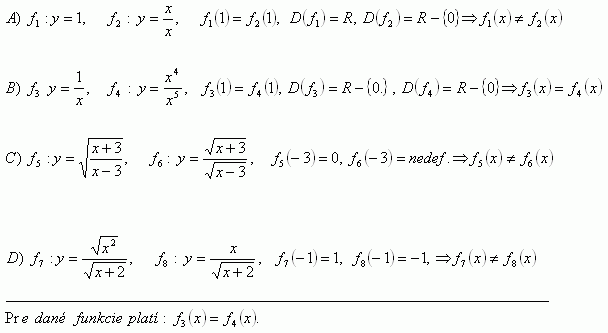
Für die gegebenen Funktionen gilt: f3(x) = F4(X)
4.Bestimmen Sie die Geradheit oder Ungeradheit der Funktionen:
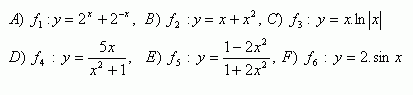
5. Bestimmen Sie, welche der folgenden Funktionen in der gegebenen Definitionsmenge beschränkt sind.
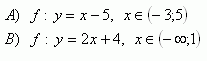
6. Bestimmen Sie für die gegebenen Funktionen die Umkehrfunktionen.
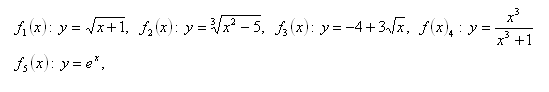
7.Bestimmen Sie die Umkehrfunktion für die Funktionen:
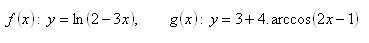
8. In der Funktion f(x): y = ax2 + bx + c , x ∈ R, bestimmen Sie a, b, c ∈ R, so dass f(0) = -3, f(-1) = -6, f(2) = 15.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
9. Bestimmen Sie b, d der Funktion f: y = (x + b):(x + d) so, dass f(1) = -1, f(-1) = -1/3
Bitte melden Sie sich an, um die Lösung anzuzeigen.
10.Bestimmen Sie die Menge aller Funktionen f(x), für die Folgendes gilt:
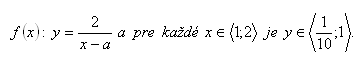
11.Die Funktion f: y= -2x +3 ist gegeben
b.) Für welche x gilt f(x) = 1, f(x) = -5
c.) Bestimmen Sie die Schnittpunkte des Graphen der Funktion mit den Koordinatenachsen
12.Geben Sie eine lineare Funktion an, deren Graph durch die Punkte verläuft
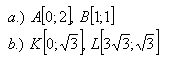
13.Laut Autohersteller ist der Kraftstoffverbrauch eines Autos pro 100 km wie folgt. Bei einer Geschwindigkeit von 80 km/h verbraucht es 6 Liter Kraftstoff, bei einer Geschwindigkeit von 110 km/h verbraucht es 8,1 Liter. Bestimmen Sie den Verbrauch des Autos bei einer Geschwindigkeit von 90 km/h.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
14.Die Funktion f: y = x2 - 4x -12 ist gegeben.
b.) Bestimmen Sie die Schnittpunkte des Graphen der Funktion mit den Koordinatenachsen
15.Geben Sie eine quadratische Funktion an, deren Elemente die geordneten Paare sind
16.Die quadratische Funktion f: y = x2 – 3x + c ist gegeben. Bestimmen Sie c so, dass die Funktion
b.) genau einen gemeinsamen Punkt mit der x-Achse hat
c.) genau zwei gemeinsame Punkte mit der x-Achse hat
17.Die quadratische Funktion f: y = x2 + 4x – 5 ist gegeben. Bestimmen Sie ihre Schnittpunkte mit den Koordinatenachsen und den Scheitelpunkt ihres Parabelgraphen.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
18.Bestimmen Sie die Koeffizienten a, b, so dass der Graph der Funktion f: y = a·log x + b durch die Punkte K, L verläuft, wobei gilt:
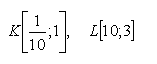
19.Bestimmen Sie die Koeffizienten a, b, so dass die Funktion f: y = a2x + b durch den Ursprung des Koordinatensystems und den Punkt M [1; 1] verläuft.
Bitte melden Sie sich an, um die Lösung anzuzeigen.20.Für welche reellen Zahlen x nehmen die Funktionen f(x) = (5!)x und g(x) = (4!)x+1 dieselben Werte an?
Bitte melden Sie sich an, um die Lösung anzuzeigen.