Würfel, Quader, Prisma und Zylinder
1. Gib die Grundformeln zur Berechnung von Volumen und Oberfläche an:
- Würfel
- Quader (Rechteckprisma)
- Prisma
- Zylinder
Würfel
a – Kante des Würfels
Volumen V = a3
Oberfläche S = 6a2
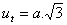
Quader
a, b, c – Kanten des Quaders
Volumen V = a·b·c
Oberfläche S = 2(ab+ac+bc)
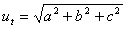
Prisma
Sp – Grundfläche
Q – Mantelfläche
v – Höhe des Prismas
Volumen V = Sp·v
Oberfläche S = 2Sp + Q
Zylinder
r – Radius der Grundfläche
v – Höhe des Zylinders
Volumen V = π·r2·v
Oberfläche S = 2πr(r+v)
Q = 2πrv
2. Zwei würfelförmige Kisten mit Kanten a = 70 cm, b = 90 cm sollen durch eine würfelförmige Kiste ersetzt werden.
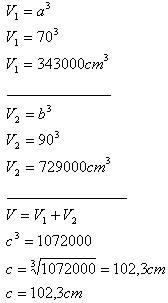
Die Kante des Ersatzwürfels beträgt c = 102,3 cm.
3. Die Kante des zweiten Würfels ist 2 cm länger als die des ersten. Der Unterschied ihrer Volumina beträgt 728 cm3.
Kante des ersten Würfels: x
Kante des zweiten Würfels: x + 2
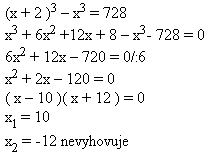
Die Kante des ersten Würfels ist 10 cm, die des zweiten 12 cm.
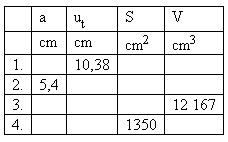
4. Ein Würfel mit der Kante a ist gegeben. Bekannte Werte stehen in der Tabelle.
5. Die Kanten zweier Würfel unterscheiden sich um 22 cm. Ihre Oberflächen unterscheiden sich um 19.272 cm2.
6. Ein Quader hat die Maße a = 4 cm, b = 3 cm, c = 5 cm.
7. Die Oberfläche eines Quaders beträgt S = 376 cm2. Seine Kanten stehen im Verhältnis a:b:c = 3:4:5.
8. Ein Wasserbehälter in Form eines Quaders enthält 1500 hl Wasser; die Wasserhöhe beträgt 2,5 m.
9. Berechne das Volumen eines Quaders, wenn seine Grundfläche S1 = 272 cm2 und seine Seitenflächen S2 = 240 cm2, S3 = 255 cm2 betragen.
Bitte melden Sie sich an, um die Lösung anzuzeigen.10. Wie groß ist die Masse einer Eisenstange (ρ = 7800 kg·m-3), die 1,5 m lang ist und einen quadratischen Querschnitt mit der Seite a = 45 mm hat?
Bitte melden Sie sich an, um die Lösung anzuzeigen.11. Die Basis eines geraden dreieckigen Prismas ist ein rechtwinkliges Dreieck mit Katheten a = 9 cm, b = 12 cm. Die Höhe des Prismas ist doppelt so groß wie die Hypotenuse der Basis.
12. Wie viel Erde muss bewegt werden, wenn ein gerader Graben von 170 m Länge mit einem gleichschenkligen Trapezquerschnitt (Basen a = 150 cm, c = 80 cm und Höhe v = 83 cm) ausgehoben wird?
Bitte melden Sie sich an, um die Lösung anzuzeigen.13. Berechne das Volumen und die Oberfläche eines Prismas, dessen Basis eine Raute mit Diagonalen u1 = 12 cm, u2 = 16 cm ist. Die Höhe des Prismas entspricht dem Doppelten der Basisseite.
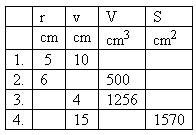
Bitte melden Sie sich an, um die Lösung anzuzeigen.14. Die Tabelle enthält Größen, die verschiedene Zylinder kennzeichnen.
15. Die Mantelfläche eines geraden Kreiszylinders, auf die in der Ebene abgerollt, ein Quadrat mit der Fläche a2 = 81 cm2 ergibt.
16. Ein gleichseitiger Zylinder (v = 2r) hat das Volumen V = 250 cm3.
17. Ein Aluminiumdraht (ρ = 2,7 g·cm-3) mit dem Durchmesser d = 3 mm hat eine Gesamtmasse von m = 1,909 kg.
18. Der äußere Umfang eines Messingrohrs (ρ = 8,5 g·cm-3) beträgt 31,4 cm. Seine Masse ist 3,14 kg und seine Länge 60 cm.