Permutationen (allgemein)
1.Definieren und charakterisieren Sie Permutationen und Permutationen mit Wiederholungen.
Lösung:
Permutationen
Eine Permutation ist eine geordnete Folge von k Elementen, die aus einer gegebenen endlichen Menge von n Zahlen ohne Wiederholungen ausgewählt wird, wobei nicht unbedingt alle n Elemente der gegebenen Menge verwendet werden müssen.
Anzahl der möglichen Permutationen:
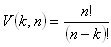
Permutationen mit Wiederholungen
Eine Permutation ist eine geordnete Folge von k Elementen, die aus einer gegebenen endlichen Menge von n Zahlen mit Wiederholungen ausgewählt wird, wobei nicht unbedingt alle n Elemente der gegebenen Menge verwendet werden müssen.
Anzahl der möglichen Permutationen mit Wiederholungen:
V*(k,n) = nk
2. Aus einer gegebenen Menge M = {a,b,c,d} alle Permutationen mit und ohne Wiederholung für k=2 auflisten. Bestimmen Sie ihre Anzahl.
a) Permutationen:
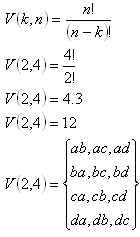
b) Permutationen mit Wiederholung:
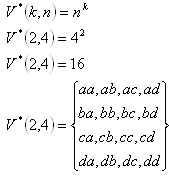
3. Es gibt 7 Mitglieder in einem Ausschuss. Auf wie viele Arten kann man einen Vorsitzenden, einen stellvertretenden Vorsitzenden, einen Sekretär und einen Kassierer wählen?
Permutationen, n = 7, k = 4
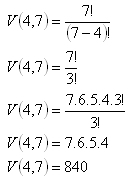
Es gibt 840 Möglichkeiten, die vier Funktionäre zu wählen.
4.Acht Schüler versprachen, sich gegenseitig eine Postkarte zu schicken. Wie viele Postkarten haben sie insgesamt verschickt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.5.Aus wie vielen Zahlen können 240 Permutationen gebildet werden, wenn die Anzahl der zu wählenden Elemente 2 beträgt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.6.Wenn die Anzahl der Mitglieder um 2 zunimmt, steigt die Anzahl der möglichen Variationen mit k=3 um 384. Wie viele Mitglieder gibt es?
Bitte melden Sie sich an, um die Lösung anzuzeigen.7. Sie haben 6 verschiedene Lose in Ihrer Tasche, nummeriert von 1 bis 6. Auf wie viele Arten können Sie 3 davon auswählen (unter Berücksichtigung der Reihenfolge), wenn
a) das ausgewählte Los nicht in die Tasche zurückgelegt wird.
b) das ausgewählte Los in die Tasche zurückgelegt wird.
8.Die Anzahl der Permutationen ohne Wiederholung mit k=3 aus x Mitgliedern ist um 225 kleiner als die Anzahl der Permutationen mit Wiederholung mit k=3 aus x Mitgliedern. Wie viele Mitglieder gibt es?
Bitte melden Sie sich an, um die Lösung anzuzeigen.