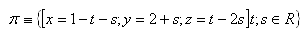Gleichung einer Ebene
1. Auf welche Weise ist eine Ebene im Raum bestimmt?
Lösung:
Eine Ebene im Raum ist durch drei verschiedene Punkte A, B, C bestimmt, die nicht auf derselben Geraden liegen.

2.Gib die allgemeine Gleichung der Ebene an, die den Punkt A [-1;5;0] enthält. Verläuft die Ebene ρ durch den Ursprung? Der Normalenvektor der Ebene ist
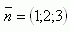
Lösung:
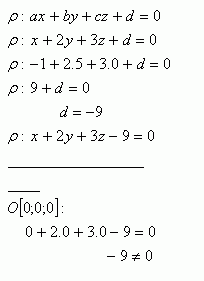
Die Ebene x + 2y + 3z - 9 = 0 verläuft nicht durch den Ursprung.
3. In der Ebene ρ liegen die drei Punkte A[2 ; -4; 5], B[3; -1;4], C[0; -10; 7]. Gib die Parameterdarstellung dieser Ebene an.
Lösung:
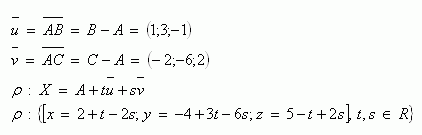
4.Die Ebene ρ ist durch Parametergleichungen gegeben. Wandle sie in die allgemeine Gleichung der Ebene um.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
5. Bestimme die Gleichung der Ebene σ, die durch den Punkt A [3;4;-5] verläuft und zu den Vektoren
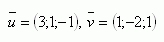
6.Bestimme die Gleichung der Ebene, die durch die Punkte A [2;-4;5], B [3;-1;4], C [0;1;6] verläuft.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
7. Bestimme die Gleichung der Ebene, die durch zwei parallele Geraden gegeben ist:
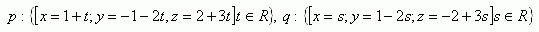
8.Gib die allgemeine Gleichung der Ebene τ an, die zur x-Achse parallel ist und durch die Punkte A[-2;-1;-3], B [2;3;0] verläuft.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
9. Bestimme die Gleichung der Ebene π, die durch den Punkt M[-4;0;4] verläuft und auf den Koordinatenachsen die Abschnitte p = 4, q = 3 abschneidet.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
10. Gegeben ist die Ebene ρ : 2x - 2y + z - 6 = 0. Berechne die Winkel zwischen ihrer Normalen und den Koordinatenachsen x, y, z.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
11.Prüfe, ob der Punkt A [22;2;–5] in der Ebene liegt
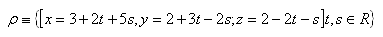
12.Bestimme die Koordinate „x“ des Punktes M [x;1,2], sodass der Punkt M in der Ebene liegt
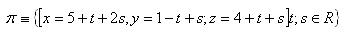
13.Gib die allgemeine Gleichung der Ebene an, die durch den Punkt A verläuft und zur Strecke AB senkrecht ist; gegeben:
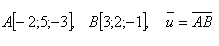
14.Gib die allgemeine Gleichung der Ebene τ an, die auf den Koordinatenachsen die Abschnitte p = 2, q = 1, r = 5 abschneidet.
p = 2, q = 1, r = 5.
15.Bestimme die Gleichung der Ebene π, die durch den Punkt M verläuft und zur Geraden p senkrecht ist. Löse für die gegebenen Daten:
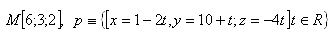
16.Zeige, dass die Punkte A, B, C, D in einer Ebene liegen. Löse für:
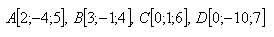
17.Gegeben sind drei Kugeln π, τ, ρ. Bestimme die allgemeine Gleichung der Ebene χ, die durch die Mittelpunkte dieser Kugeln verläuft. Es gilt:
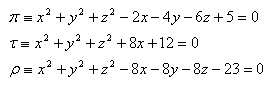
18.Gib die allgemeine Gleichung der Ebene π an, die durch die Punkte
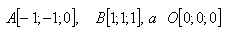
19.Wandle die Parameterform der Ebene μ in die allgemeine Form um; gegeben ist
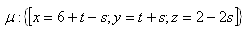
20.Für welchen Wert des Parameters „m“ aus ℝ liegt der Punkt M[0;6;m] in der Ebene