Vektor im Raum

1. Welche Eigenschaften hat ein Vektor im Raum?

Lösung:

Vektor

A(a1,a2,a3), B(b1,b2,b3),u⃗=AB→=B−A=(b1−a1, b2−a2, b3−a3)=(u1,u2,u3)

∣u⃗∣=u12+u22+u32|\vec{u}| = \sqrt{u_1^2 + u_2^2 + u_3^2}

S=A+B2,S(a1+b12, a2+b22, a3+b32)S = \frac{A + B}{2},\quad S\left( \frac{a_1 + b_1}{2},\; \frac{a_2 + b_2}{2},\; \frac{a_3 + b_3}{2} \right)

ku⃗=(ku1,ku2,ku3)k\vec{u} = (k u_1, k u_2, k u_3)

Skalarprodukt (Punktprodukt) zweier Vektoren

u⃗=(u1,u2,u3),v⃗=(v1,v2,v3)\vec{u} = (u_1, u_2, u_3),\quad \vec{v} = (v_1, v_2, v_3)

u⃗⋅v⃗=∣u⃗∣ ∣v⃗∣cos⁡φ=u1v1+u2v2+u3v3\vec{u} \cdot \vec{v} = |\vec{u}|\,|\vec{v}| \cos \varphi = u_1 v_1 + u_2 v_2 + u_3 v_3

Winkel zwischen zwei Vektoren cos⁡φ=u1v1+u2v2+u3v3∣u⃗∣ ∣v⃗∣\cos \varphi = \frac{u_1 v_1 + u_2 v_2 + u_3 v_3}{|\vec{u}|\,|\vec{v}|}


 

Bedingung dafür, dass zwei Vektoren senkrecht sind

u1v1+u2v2+u3v3=0u_1 v_1 + u_2 v_2 + u_3 v_3 = 0

Vektorprodukt (Kreuzprodukt) zweier Vektoren

u⃗=(u1,u2,u3),v⃗=(v1,v2,v3)\vec{u} = (u_1, u_2, u_3), \quad \vec{v} = (v_1, v_2, v_3)w⃗=u⃗×v⃗=(u2v3−v2u3, u3v1−v3u1, u1v2−v1u2)\vec{w} = \vec{u} \times \vec{v} = (u_2 v_3 - v_2 u_3,\; u_3 v_1 - v_3 u_1,\; u_1 v_2 - v_1 u_2)w⃗⊥u⃗undw⃗⊥v⃗\vec{w} \perp \vec{u} \quad \text{und} \quad \vec{w} \perp \vec{v}

Lineare Abhängigkeit

Vektoren sind linear abhängig, wenn es reelle Zahlen k,l,m,…k, l, m, \ldots gibt – mindestens eine davon ungleich null –, sodass:

ku⃗+lv⃗+mw⃗=0⃗k\vec{u} + l\vec{v} + m\vec{w} = \vec{0}

2.Bestimme die Länge der Strecke AB, deren Mittelpunkt S im Ursprung der Koordinatenachsen liegt und deren Punkt A [6; -2; 3] ist.

Lösung:

vektor-v-priestore-2

Die Länge der Strecke ist |AB| = 14j

3.Bestimme die Koordinaten des Eckpunkts C [c1; c2; c3] im Dreieck ΔABC, wenn die Eckpunkte und der Schwerpunkt gegeben sind: A [3;3;3], B [-2;1;2], T [0;-1;0]. Bestimme außerdem den Umfang dieses Dreiecks.

Lösung:

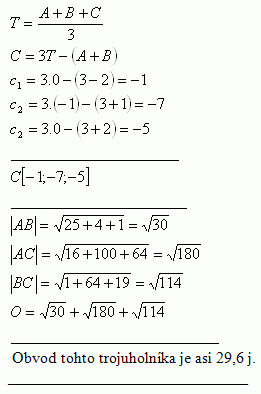
vektor-v-priestore-3

Der Umfang des Dreiecks ist ungefähr 29,6 j.

4.Bestimme auf der z-Achse den Punkt, der von den Punkten A [ -2;1;4] und B [3;0;1] gleich weit entfernt ist.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

5. Im Parallelepiped ABCDEFGH sind die Koordinaten der Punkte A[2;-3;1], B[3;-4;2], D[4;2;-3], E[5;3;4] bekannt. Berechne die Koordinaten der übrigen Punkte C, F, H, G.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

6.Beweise, dass das Dreieck ΔABC gleichschenklig und rechtwinklig ist, wenn: A[2;-4;9], B[-1;-4;5], C[6;-4;6]

Bitte melden Sie sich an, um die Lösung anzuzeigen.

7.Gegeben sind die Vektoren:

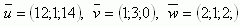
 vektor-v-priestore-7z

Bestimme, ob sie linear abhängig sind.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

8.Untersuche, ob die gegebenen vier Punkte in einer Ebene liegen. A[1;2;-1], B[0;1;5], C[-1;2;1], D[2;1;3]

Bitte melden Sie sich an, um die Lösung anzuzeigen.

9.Berechne den Flächeninhalt des Dreiecks ΔABC, dessen Eckpunkte in den Punkten liegen:

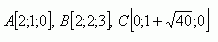
vektor-v-priestore-9z
Bitte melden Sie sich an, um die Lösung anzuzeigen.

10.Berechne das Volumen der viereckigen Pyramide ABCDV, deren Eckpunkte gegeben sind: A[2;0;0], B[0;3;0], D[0;0;6], V[2;3;8]

Bitte melden Sie sich an, um die Lösung anzuzeigen.

11. Bestimme die Länge der Seitenhalbierenden im Dreieck ABC, wenn A[1;0;2], B[-2;1;-3], C[0;-1;1].

Bitte melden Sie sich an, um die Lösung anzuzeigen.

12. Bestimme den Abstand der Mittelpunkte der Strecken AB und CD, wenn:

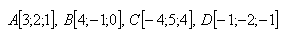
vektor-v-priestore-12z.gif
Bitte melden Sie sich an, um die Lösung anzuzeigen.

13.Seien A[1;2;8] und B[4;y;4], und |AB| = 5. Wie groß ist y?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

14. Gegeben sind die Punkte K, L, M, N. Berechne die Koordinaten des Punktes N, wenn:

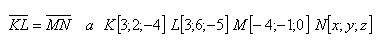
vektor-v-priestore-14z.gif
Bitte melden Sie sich an, um die Lösung anzuzeigen.

15.Gegeben sind die Punkte A[4;-3;2], B[5;0;-1]. Bestimme die Zahlen m, n, so dass der Punkt C[2;m;n] auf dem Vektor AB liegt.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

16.Bestimme die gegenseitige Lage (Beziehung) der Vektoren

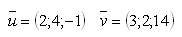
vektor-v-priestore-16z.gif
Bitte melden Sie sich an, um die Lösung anzuzeigen.

17. Gegeben sind drei Punkte im Raum A, B, C. Berechne das Maß des Winkels

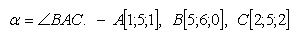
vektor-v-priestore-17z.gif
Bitte melden Sie sich an, um die Lösung anzuzeigen.

18.Berechne Umfang und Flächeninhalt des Dreiecks ABC, wenn seine Eckpunkte sind:

A[0;1;2], B[1;2;0], C[2;0;1]
Bitte melden Sie sich an, um die Lösung anzuzeigen.

19. Im Dreieck ABC sind die Eckpunkte A, B und der Schwerpunkt T gegeben. Bestimme die Koordinaten des Eckpunkts C, wenn

A[3;3;3], B[-2;1;2], T[0;-1;0], C[x,y,z]
Bitte melden Sie sich an, um die Lösung anzuzeigen.

20.Stelle den Vektor u als Linearkombination der Vektoren v und w dar, wenn:

vektor-v-priestore-20z.gif
Bitte melden Sie sich an, um die Lösung anzuzeigen.