Geraden in einer Ebene
1. Erkläre die verschiedenen Arten von Geradengleichungen in einer Ebene.
- Parameterform
- Allgemeine Form
- Steigungsform
- Abstand eines Punktes von einer Geraden
Lösung:
a) Parameterform:

2. Schreibe die Gleichung der Geraden, die durch die Punkte A[2;7] und B[5;1] verläuft, in der Form:
b) Allgemeine Form
c) Steigungsform
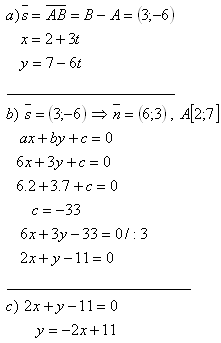
3. Schreibe die Gleichung der Geraden, auf der der Mittelpunkt der Strecke AB liegt, wenn A[1;5] und B[7;3].
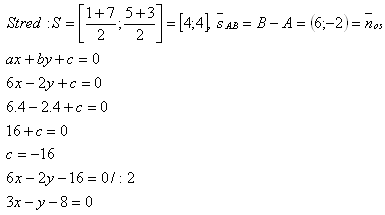
4. Schreibe die Gleichung der Geraden, auf der die Höhe vc im Dreieck A[5;6], B[-2;4] und C[6;-1] liegt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.5. Die Gerade (2–m)x + 3my + (2m-6) = 0 ist gegeben.
a) die Gerade durch den Ursprung verläuft
b) die Gerade parallel zur x-Achse ist
c) die Gerade parallel zur y-Achse ist
6. Die Gerade ist gegeben durch p: 4x – 3y +6 = 0
b) wandle sie in die Parameterform um
c) berechne den Abstand des Punktes, der nicht auf der Geraden liegt, von der Geraden
7. Schreibe die Gleichung einer Geraden, die parallel zur Geraden p: 5x +12y -1 = 0 ist und in einem Abstand d = 5 Einheiten von ihr liegt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.8. Das Dreieck hat die Eckpunkte A[-1;-5], B[9;-1] und C[1;7].
a) Gleichung der Seite c = AB
b) Gleichung der Medianen tc
c) Gleichung der Höhe auf Seite c, vc
9. Schreibe die Gleichung der Geraden, die mit der x-Achse einen Winkel φ = 135° bildet und durch den Punkt A[3;-1] verläuft.
10. Ein Lichtstrahl stammt aus der Quelle A[-1;-5], reflektiert sich an der x-Achse wie an einem Spiegel und verläuft durch den Punkt B[9;-5].
11. Die Scheitelpunkte eines Dreiecks A und B sowie der Schnittpunkt der Höhen Q sind gegeben. Bestimme die Koordinaten des Scheitelpunkts C des Dreiecks, wenn
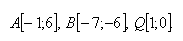
12. Finde auf der Geraden p den Punkt C, der von den Punkten A und B gleich weit entfernt ist.
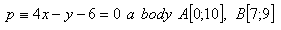
13. Berechne die Länge der Höhe va im Dreieck ABC, wenn seine Seiten die folgenden Gleichungen haben:
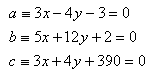
14. Gegenüberliegende Seiten des Quadrats ABCD liegen auf parallelen Geraden.
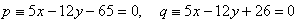
Berechne den Umfang und die Fläche dieses Quadrats.
15. Bestimme den Umfang und die Fläche des rechtwinkligen Dreiecks, das durch die Gerade 3x + 4y –12 = 0 auf den Koordinatenachsen ausgeschnitten wird.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
16. Schreibe die Gleichung einer Geraden, die zu 5x + 12y -1 =0 parallel ist und im Abstand d = 5 liegt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
17. Berechne den Abstand des Punktes A[2;-4] von der Geraden 3x + 4y = 0.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
18. Die Diagonalen einer Raute u1 = 4, u2 = 6 liegen auf den Koordinatenachsen (u1 auf der x-Achse). Schreibe die Gleichungen der Geraden, auf denen die Seiten der Raute liegen.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
19. Bestimme die Gleichung einer Geraden, die durch den Punkt [2;3] verläuft, so dass das Segment auf der x-Achse halb so lang ist wie das Segment auf der y-Achse.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
20. Gegeben sind die Punkte A[3;-2], B[1;4], C[-1;-3]. Bestimme den Punkt D so, dass die Gerade CD das Segment AB in seinem Mittelpunkt S schneidet und CD = 3·|CS| gilt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
⁞