Vektor in der Ebene
1.Charakterisieren Sie die Eigenschaften eines Vektors in der Ebene:

2.Gegeben sind die Punkte A[-2;5], B[1;yB] und C[4;-3]. Bestimmen Sie B, sodass Folgendes gilt:
b) die Vektoren AB und AC parallel sind
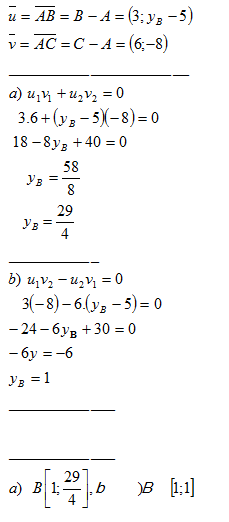
3.Gegeben ist der Vektor v = AB wie folgt: A[1;1], B[b1;b2] und der Mittelpunkt des Vektors S[4;5].
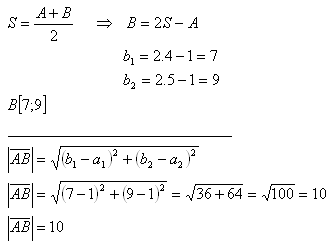
Der Punkt B hat die Koordinaten B[7;9]. Die Länge des Vektors beträgt 10 Einheiten.
4.Die Punkte A[2;-3] und B[x;0] sind gegeben.
5.Weisen Sie nach, dass das Dreieck mit den Eckpunkten A[-3;-2], B[1;4] und C[-5;0] gleichschenklig ist.
Bitte melden Sie sich an, um die Lösung anzuzeigen.6.Gegeben sind die Vektoren a = (3;-2) und b = (-1;5).
a·c = 17
b·c = 3
7.Bestimmen Sie den Vektor v, der zum Vektor u = (3;4) senkrecht ist und dessen Länge 15 beträgt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.8.Die Eckpunkte des Dreiecks ΔABC sind die Punkte A[1;1], B[2;-1] und C[3;2].
9.Bestimmen Sie auf den Koordinatenachsen den Punkt, der vom Punkt A [4;-6] den Abstand 5 hat.
Bitte melden Sie sich an, um die Lösung anzuzeigen.10.Die Eckpunkte des Vierecks liegen in den Punkten: A[0;0], B[3;-4], C[6;0] und D[3;4].
11.Die Punkte A, B, C sind die Eckpunkte des Dreiecks ABC. Zeigen Sie, dass das Dreieck ABC gleichseitig ist. Berechnen Sie seine Fläche.
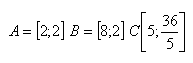
12.Die Punkte A, B, C sind die Eckpunkte des Dreiecks ABC. Bezeichnen Sie die Mittelpunkte der Seiten AC, BC mit M,N. Zeigen Sie, dass die Mittellinie MN zur Seite AB parallel ist und dass MN = 0,5·AB gilt.
13.Gegeben ist das gleichschenklige Trapez ABCD mit Eckpunkten
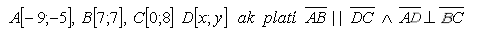
Bestimmen Sie die Koordinaten des Punktes D.
14.Bestimmen Sie die Koordinaten des Mittelpunktes S und die Größe des Radius r des Kreises, der durch die Punkte A,B,C geht. Lösen Sie für die Punkte:
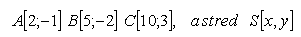
15.Bestimmen Sie die Koordinaten des Schwerpunkts eines Systems aus vier gleich schweren Körpern, die in den Punkten A,B,C,D liegen. Der Schwerpunkt T ist der Mittelpunkt der Strecke, deren Endpunkte an den Mittelpunkten der Vektoren liegen
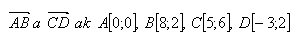
16.Der Punkt A [2;5] ist der Angriffspunkt der Kraft F, deren Projektion auf die Koordinatenachsen x = 3; y = 3 ist. Berechnen Sie das Ende des Vektors, der die Kraft F darstellt.
17.Gegeben sind drei Punkte A,B,
- a.) Weisen Sie nach, dass sie auf derselben Geraden liegen
- b.) Bestimmen Sie das Verhältnis der Beträge der Vektoren
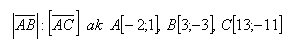
18.Ein gleichschenkliges Dreieck ABC hat die Basis AB mit Eckpunkt A und Basismittelpunkt S. Sein Eckpunkt C liegt auf der x-Achse. Bestimmen Sie die Eckpunkte B und C des Dreiecks.
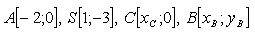
19.Gegeben ist der Vektor u = (5;-3) und der Vektor v = (1;yv) mit
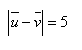
Bestimmen Sie yv
20.Die Punkte A,B,C sind die Eckpunkte des Dreiecks ABC und die Punkte M,N,P sind die Mittelpunkte seiner Seiten. Bestimmen Sie die Koordinaten dreier Vektoren, deren Lage mit den Seitenhalbierenden des Dreiecks ABC zusammenfällt, wobei der Startpunkt jeweils im Eckpunkt des Dreiecks liegt. Berechnen Sie die Längen dieser Vektoren.