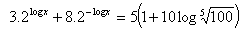Logarithmische Exponentialgleichungen
1. Löse:
log3(2x - 7) = 2 2x > 7
Lösung:
log3(2x - 7) = 2
log3(2x - 7) = log332
2x – 7 = 32
2x – 7 = 9
2x = 16
2x = 24
x = 4
K = {4}
log3(2x - 7) = 2
log3(2x - 7) = log332
2x – 7 = 32
2x – 7 = 9
2x = 16
2x = 24
x = 4
K = {4}
2. Löse:
log2( 9- 2x) = 3 – x 2x < 9
Lösung:
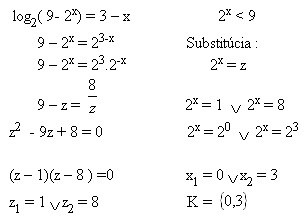
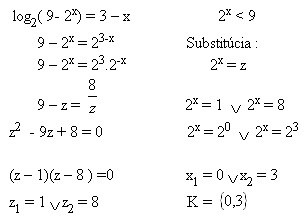
3. Löse:
log3( 1 + log3(2x-7)) = 1 2x > 7
Lösung:
log3( 1 + log3(2x-7)) = 1
log3( 1+ log3(2x-7)) = log33
1 + log3(2x-7) = 3
log3(2x-7) = 2
log3(2x-7) = log39
2x-7 = 9
2x = 16
2x = 24
x = 4
K = {4}
log3( 1 + log3(2x-7)) = 1
log3( 1+ log3(2x-7)) = log33
1 + log3(2x-7) = 3
log3(2x-7) = 2
log3(2x-7) = log39
2x-7 = 9
2x = 16
2x = 24
x = 4
K = {4}
4. Löse:
log3(3x- 8) = 2 – x 3x > 8
Bitte melden Sie sich an, um die Lösung anzuzeigen. 5. Löse:
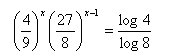
6. Löse:
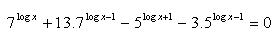
7. Löse:
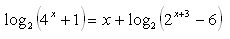
8. Löse:
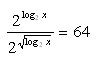
9. Löse:
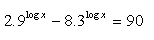
10. Löse:
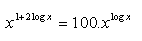
11. Löse in reellen Zahlen:
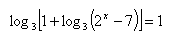
12. Löse in reellen Zahlen:
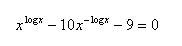
13. Löse in reellen Zahlen:
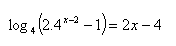
14. Löse in reellen Zahlen:
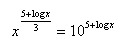
15. Löse in reellen Zahlen:
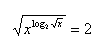
16. Löse in reellen Zahlen:
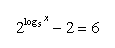
17. Löse in reellen Zahlen:
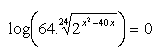
18. Löse in reellen Zahlen:
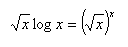
19. Löse in reellen Zahlen:
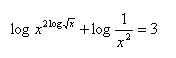
20. Löse in reellen Zahlen: