Rechtwinkliges Dreieck
1. Definiere ein rechtwinkliges Dreieck.
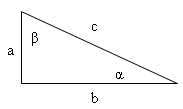
a) Satz des Pythagoras:
a2 + b2 = c2
b) Goniometrische Funktionen:
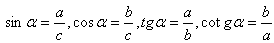
c) Umfang:
U = a + b + c
d) Fläche:
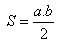
e) Euklidische Sätze:
a2 = c·ca
b2 = c·cb
v2 = ca·cb
2. Die Katheten eines rechtwinkligen Dreiecks ΔABC sind a = 3 cm, b = 4 cm.
a) Länge der Hypotenuse c
b) Höhe auf die Hypotenuse, vc
c) Fläche S
d) Die spitzen Winkel α und β
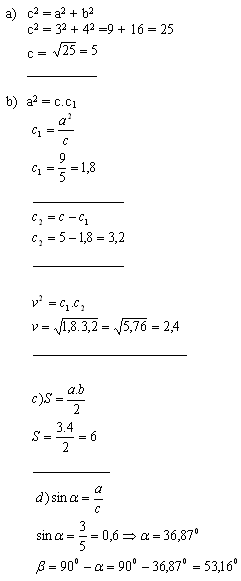
Für das Dreieck ΔABC gilt: c = 5 cm, vc = 2,4 cm, S = 6 cm2, α = 36,87°, β = 53,16°.
3. Seien a, b die Katheten eines rechtwinkligen Dreiecks und c die Hypotenuse, α der Winkel gegenüber von a.
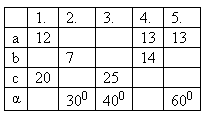

4. Die Seiten eines rechtwinkligen Dreiecks bilden eine arithmetische Folge. Bestimme:
b) die Fläche
des Dreiecks. Die längere Kathete ist 16 cm lang.
5. Die Summe der Katheten eines rechtwinkligen Dreiecks beträgt 30 cm. Die Fläche beträgt 110,5 cm2. Bestimme den Umfang des Dreiecks.
Bitte melden Sie sich an, um die Lösung anzuzeigen.6. Die Schenkel eines gleichschenkligen Dreiecks sind 1 cm länger als die Basis. Die Höhe ist 2 cm kürzer als der Schenkel. Bestimme die Länge des Schenkels.
Bitte melden Sie sich an, um die Lösung anzuzeigen.7. Die Seiten eines Dreiecks haben die Längen a = 4p2 - 1, b = 4p, c = 4p2 + 1. Zeige, dass es sich um ein rechtwinkliges und pythagoreisches Dreieck handelt. Schreibe vier pythagoreische Dreiecke auf.
Bitte melden Sie sich an, um die Lösung anzuzeigen.8. Wie groß ist die Steigung einer Straße, wenn das Verkehrsschild 6,7 % angibt? Das Auto fährt 2,3 km auf dieser Straße.
9. Berechne die Fläche eines gleichschenkligen rechtwinkligen Dreiecks, dessen Umfang 20 cm beträgt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.10. Für die Katheten eines rechtwinkligen Dreiecks gilt a : b = 2 : 3. Die Hypotenuse ist 10 cm lang.