Statistik
1. Erkläre die folgenden Begriffe:
- Verteilungskennwerte (Durchschnitt)
- Streuungskennwerte
Lösung:
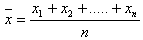
b) Geometrisches Mittel:
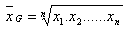
c) Harmonisches Mittel:
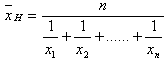
d) Modus mod(x) ist der Wert, der in einer Datenreihe oder Wahrscheinlichkeitsverteilung am häufigsten vorkommt.
e) Median med(x) ist:
R = xmax - xmin
b) Varianz (Streuung)
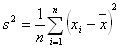
c) Standardabweichung
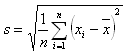
Verteilungskennwerte
a) Arithmetisches Mittel: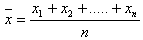
b) Geometrisches Mittel:
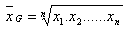
c) Harmonisches Mittel:
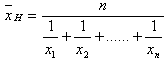
d) Modus mod(x) ist der Wert, der in einer Datenreihe oder Wahrscheinlichkeitsverteilung am häufigsten vorkommt.
e) Median med(x) ist:
- der mittlere Wert einer der Größe nach geordneten Datenreihe mit ungerader Anzahl von Elementen
- das arithmetische Mittel der beiden mittleren Werte einer der Größe nach geordneten Datenreihe mit gerader Anzahl von Elementen
Streuungskennwerte
a) SpannweiteR = xmax - xmin
b) Varianz (Streuung)
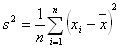
c) Standardabweichung
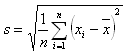
2. Folgende Werte wurden im Labor gemessen (in Millimetern):
{302;310;312;310;313;318;305;309;310;309}
Bestimme das arithmetische Mittel, das geometrische Mittel, den Modus und den Median.
Lösung:
Sortierte Werte:
{302;305;309;309;310;310;310;312;313;318}
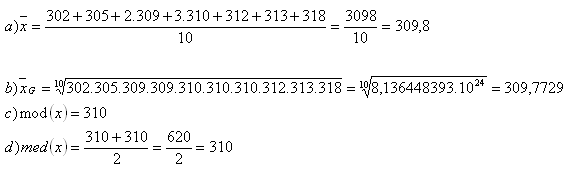
Sortierte Werte:
{302;305;309;309;310;310;310;312;313;318}
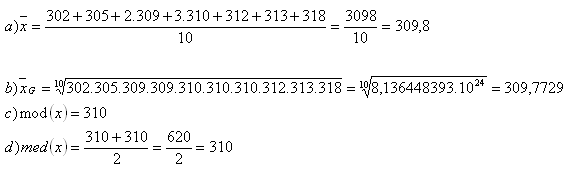
3.Ein Auto fuhr in der ersten Hälfte der Strecke mit einer Durchschnittsgeschwindigkeit von v1 = 20 km/h und in der zweiten Hälfte mit v2 = 80 km/h. Bestimme die Durchschnittsgeschwindigkeit des Autos.
Lösung:
Das Auto fuhr mit unterschiedlichen Geschwindigkeiten, daher legte es jede Hälfte der Strecke in unterschiedlicher Zeit zurück.
Die Durchschnittsgeschwindigkeit entspricht dem harmonischen Mittel von v1 und v2.
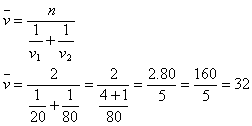
Die Durchschnittsgeschwindigkeit des Autos betrug 32 km/h.
Das Auto fuhr mit unterschiedlichen Geschwindigkeiten, daher legte es jede Hälfte der Strecke in unterschiedlicher Zeit zurück.
Die Durchschnittsgeschwindigkeit entspricht dem harmonischen Mittel von v1 und v2.
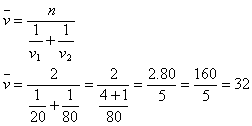
Die Durchschnittsgeschwindigkeit des Autos betrug 32 km/h.
4.Folgende Werte wurden zur Bestimmung des Gewichts eines Zahnrads gemessen. Finde das Intervall, das den tatsächlichen Gewichtswert mit einer Wahrscheinlichkeit von 68 % enthält.
M = {324;330;327;319;334;304}
Bitte melden Sie sich an, um die Lösung anzuzeigen. 5. Die Schützen A und B treten im Zielschießen gegeneinander an. Wer war präziser und gewann den Wettbewerb?
Ergebnisse:
A = {9;8;8;8;7}
B = {10;10;8;7;5}
Bitte melden Sie sich an, um die Lösung anzuzeigen. A = {9;8;8;8;7}
B = {10;10;8;7;5}