Bestimmtes Integral in der Physik
1.Ein Teilchen bewegt sich auf einer geraden Linie mit der Beschleunigung a = 2.6 m·s-2. Bestimmen Sie die Geschwindigkeitsgleichung und die Weggleichung (wenn v0 = 0, s0 = 0). Berechnen Sie die Geschwindigkeit und den Weg zur Zeit t = 2 s.
Lösung:
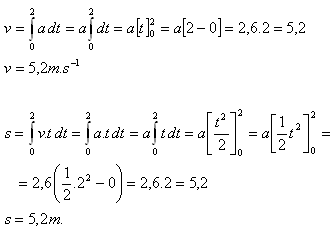
2.Bestimmen Sie die Arbeit, die erforderlich ist, um eine Feder aus ihrem ungespannten Zustand um 25 cm zu dehnen, wenn eine Kraft von 16 N parallel zur Federachse sie um 80 cm dehnt.
Lösung:
F = 16 N, x = 80 cm = 0.8 m, a = 0, b = 25 cm = 0.25 m.
Die Kraft F ist proportional zur Dehnung x.
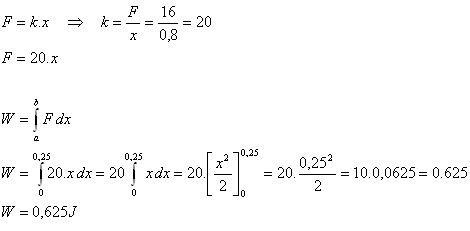
3.Bestimmen Sie den Effektivwert eines sinusförmigen Wechselstroms.
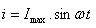
Lösung:
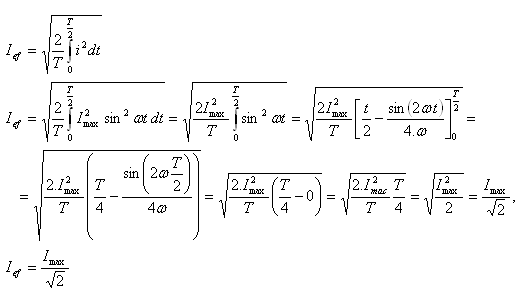
4.Durch eine Herdspule mit Widerstand R fließt ein Wechselstrom mit dem Maximalwert Imax. Leiten Sie die Formel zur Berechnung der Joule'schen Wärme ab. Der momentane Strom ist: i = Imax sin ωt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
5.Welche Strecke legt ein Körper zurück, der sich mit der Geschwindigkeit v = At2 + Bt + C während der ersten 10 Sekunden bewegt, wenn:
- A = 3 m·s-1
- B = 1 m·s-1
- C = –1 m·s-1
6.Berechnen Sie die Strecke, die ein Regentropfen in den ersten 6 Sekunden zurücklegt. Luftwiderstand wird vernachlässigt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
7. Welche Arbeit muss verrichtet werden, damit ein Körper der Masse m seine Geschwindigkeit von v1 auf v2 erhöht?
Bitte melden Sie sich an, um die Lösung anzuzeigen.8.Welche Arbeit verrichtet eine äußere Kraft beim elastischen Dehnen einer Stahlstange der Länge l0 = 2 m und des Querschnitts S = 5 mm2 um 1 mm?
Bitte melden Sie sich an, um die Lösung anzuzeigen.9.Berechnen Sie die Arbeit, die erforderlich ist, um einen Körper der Masse m auf die Höhe h über der Erdoberfläche zu heben. Verwenden Sie die Beziehung:
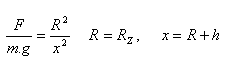
10. Wie lange dauert es, bis Wasser, das in ein zylindrisches Gefäß mit der Grundfläche S = 420 cm2 und der Wasserhöhe h = 40 cm gegossen wurde, durch eine Öffnung am Boden abfließt? Die Öffnung hat die Fläche s = 2 cm2. Die Ausflussgeschwindigkeit ist gegeben durch:
- v = μ·s·(2·g·x)1/2
11.Berechnen Sie die Koordinaten des Schwerpunkts eines Quadrats mit der Seitenlänge a = 6 cm.
Bitte melden Sie sich an, um die Lösung anzuzeigen.12.Berechnen Sie die Koordinaten des Schwerpunkts der ebenen Figur, die durch die Funktion begrenzt ist:
- f(x) = y = x3, für x ∈ < 0 ,1 >
13. Berechnen Sie die Koordinaten des Schwerpunkts der ebenen Figur, die begrenzt wird durch:
- die Parabel y = x2
- und die Geraden y = 0, x = 1.
14.Bestimmen Sie die Koordinaten des Dreiecks ΔABO, das gebildet wird von:
- der Geraden y = –x + 6 im Koordinatensystem. A[6 , 0], B[0 ,6], O[0, 0]
15. Finden Sie die Koordinaten des Schwerpunkts der ebenen Figur, die durch die Kurve begrenzt wird:
- a2y = b x2 für x ∈ < 0 ; a >