Dispersion und Polarisation des Lichts
1. Erkläre die Dispersion und Polarisation des Lichts.
Lösung:
Zerlegung des Lichts
Weißes Licht ist eine Mischung aus sieben monochromatischen Farben (Rot, Orange, Gelb, Grün, Blau, Indigo, Violett), d. h. eine Mischung aus elektromagnetischen Wellen mit unterschiedlichen Frequenzen.
| R | O | Gb | Gr | B | I | V |
|---|---|---|---|---|---|---|
| f (10¹⁴ Hz) | 4.6 | 5.0 | 5.2 | 5.75 | 6.7 | 7.0 |
Einzelne farbige Lichtstrahlen breiten sich in einem Medium mit unterschiedlichen Geschwindigkeiten aus ,
daher besitzen sie unterschiedliche Brechungsindizes und werden unter verschiedenen Winkeln gebrochen.
Polarisation des Lichts
Natürliches Licht ist unpolarisiert. Es ist eine transversale elektromagnetische Welle, die durch Schwingungen zueinander senkrechter Vektoren
gekennzeichnet ist. Auf der Netzhaut des Auges wirken nur die Schwingungen des Vektors der elektrischen Feldstärke .
Im polarisierten Licht erfolgen die Schwingungen des Vektors in einer einzigen Ebene.
Eine vollständige Polarisation tritt auf, wenn der Einfallswinkel der sogenannte Brewster-Winkel ist.
Beim Polarisationswinkel steht der reflektierte Strahl senkrecht auf dem gebrochenen Strahl.
2.Die Wellenlänge der Wasserstofflinie H2 in Luft ist λ0 = 656.4 nm. Wie groß ist ihre Wellenlänge in Wasser? (n = 1.33)
Lösung:
Analyse:
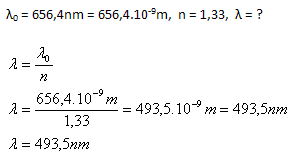
Die Wellenlänge der Wasserstofflinie H2 in Wasser beträgt λ = 493.5 nm.
3. Bestimme, ob die Geschwindigkeit, mit der sich Licht ausbreitet, von seiner Frequenz abhängt.
b) in einem Medium,
Lösung:
a) Im Vakuum:
b) In einem Medium:
Im Vakuum hängt die Geschwindigkeit des Lichts nicht von der Frequenz ab, in einem Medium hingegen schon.
4. Leite die Formel zur Berechnung des Brewster-Winkels – des Winkels vollständiger Polarisation – her.
Bitte melden Sie sich an, um die Lösung anzuzeigen.5. Der Winkel vollständiger Polarisation für opake Emaille beträgt αp = 58°. Wie groß ist der Brechungsindex der Emaille? (n1=1, n2=?)
Bitte melden Sie sich an, um die Lösung anzuzeigen.
6. Berechne den Brewster-Winkel der vollständigen Polarisation für:
- Wasser: n = 1.33
- Glas: n = 1.5
- Diamant: n = 2.465
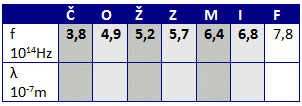
7.Vervollständigen Sie die Tabelle der Lichtdispersion:
| R | O | Gb | Gr | B | I | V |
|---|
8.Ein Lichtstrahl fällt aus der Luft auf die Wasseroberfläche unter einem Einfallswinkel α = 70o. Bestimmen Sie, welcher der farbigen Strahlen (rot oder violett) sich am wenigsten bzw. am stärksten von der ursprünglichen Richtung des Lichtstrahls vor dem Auftreffen auf das Wasser ablenkt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.9.Eine Diamantplatte (n = 2.465) wird mit der violetten Komponente des Lichts (f = 7.8·1014 Hz) beleuchtet. Bestimmen Sie die Wellenlänge der violetten Lichtkomponente im Vakuum und im Diamanten.
Bitte melden Sie sich an, um die Lösung anzuzeigen.10.Der Winkel der vollständigen Polarisation für Diamant beträgt αP = 68o. Wie groß ist der Brechungsindex des Diamanten? Unter welchem Winkel wird ein monochromatischer Lichtstrahl gebrochen, wenn sein Einfallswinkel dem Winkel der vollständigen Polarisation entspricht?
Bitte melden Sie sich an, um die Lösung anzuzeigen.11.Unter welchem Einfallswinkel tritt vollständige Polarisation auf, wenn Licht an der Grenzfläche von Eis (n1 = 1.308) und Wasser (n2 = 1.333) reflektiert wird?
Bitte melden Sie sich an, um die Lösung anzuzeigen.