Elektromagnetischer Oszillator
1. Gib die Zusammensetzung und die Eigenschaften eines elektromagnetischen Oszillators an.
Lösung:
Ein elektromagnetischer Oszillator ist ein Wechselstromkreis mit einer Spule (Induktivität) und einem Kondensator (Kapazität). Er wird auch Schwingkreis oder LC-Schwingkreis genannt. Im Schwingkreis wird elektrische Energie periodisch in magnetische Energie umgewandelt und zurück. Dabei entstehen elektromagnetische Schwingungen. Für die Frequenz des elektromagnetischen Oszillators (die Eigenfrequenz des Schwingkreises) gilt die Thomson-Beziehung:

-
= Induktivität der Spule
-
= Kapazität des Kondensators
2. Wie ändert sich die Schwingungsfrequenz des LC-Schwingkreises, wenn wir die Platten des Kondensators näher zusammenbringen?
Lösung:
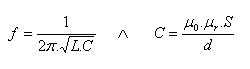
Wenn wir die Platten des Kondensators im Schwingkreis näher zusammenbringen, wird d kleiner, C größer und die Frequenz f kleiner.
3.Die Schwingkreise haben folgende Parameter:
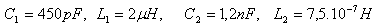
Welcher Schwingkreis schwingt mit der höheren Frequenz?
Lösung:
Analyse:
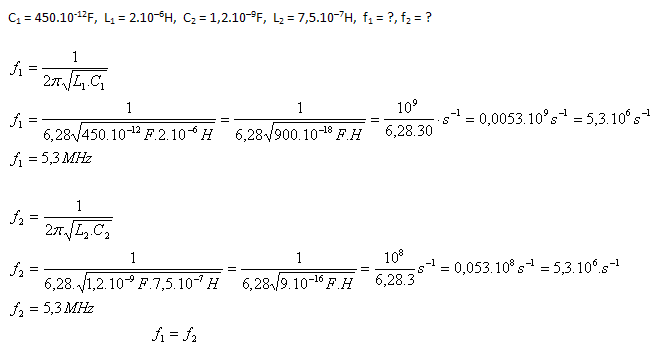
Beide LC-Schwingkreise schwingen mit derselben Frequenz, f1 = f2 = 6,3 MHz.
4.Ein Schwingkreis besteht aus einem Kondensator mit der Kapazität C = 10 μF und einer Spule mit veränderlicher Induktivität. In welchem Bereich muss die Induktivität der Spule liegen, damit die Eigenfrequenz des Schwingkreises von 400 Hz bis 500 Hz variiert?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
5.Der Schwingkreis besteht aus einer Spule mit der Induktivität L = 3 mH und einem Plattenkondensator, dessen Platten Scheiben mit dem Radius 1,2 cm sind. Der Plattenabstand beträgt 0,3 mm. Bestimme die Periodendauer des Schwingkreises. Wie ändert sich die Periode, wenn wir ein Dielektrikum mit εr = 4 zwischen die Platten einfügen?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
6.Wir schließen einen Kondensator mit der Kapazität C1 an eine Spule mit konstanter Induktivität L an. Wir stellen fest, dass der Oszillator mit der Eigenfrequenz f1 = 100 kHz schwingt. Wenn wir einen Kondensator mit der Kapazität C2 an diese Spule anschließen, schwingt der Oszillator mit der Eigenfrequenz f2 = 160 kHz. Welche Eigenfrequenz hat der Oszillator, wenn wir beide Kondensatoren an die Spule anschließen
- a) parallel
- b) in Reihe
7.Die Spannung an den Platten eines Kondensators in einem Schwingkreis ändert sich nach der Gleichung u = 50cos (104π·t) (V). Die Kapazität des Kondensators beträgt C = 0,1 μF. Berechnen Sie die Schwingungsperiode T des Kreises und schreiben Sie die Gleichung für den momentanen Wert des Stroms.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
8.Der Schwingkreis besteht aus einem Kondensator mit der Kapazität C = 24 nF und einer Spule mit der Induktivität L = 0.6 H. Im Anfangsmoment ist der Kondensator auf die Spannung Umax = 50 V aufgeladen. Schreiben Sie die Gleichung für den momentanen Wert des Stroms im Kreis.
Bitte melden Sie sich an, um die Lösung anzuzeigen.9.Der momentane Wert des Stroms in einem Schwingkreis ist durch die Gleichung i = 0,01·sin (ω t) (A) gegeben. Berechnen Sie die Energie des Magnetfelds der Spule zum Zeitpunkt t = T/8 s. Der Schwingkreis enthält eine Spule mit der Induktivität
L = 0.6 H.
10.Der momentane Wert der Spannung in einem Schwingkreis ist durch die Gleichung u = 50·cos (ω·t) (V) gegeben. Berechnen Sie die Energie des elektrischen Feldes eines Kondensators mit der Kapazität C = 24 nF zum Zeitpunkt t = T/8 s.
Bitte melden Sie sich an, um die Lösung anzuzeigen.11.Ein Schwingkreis, in dem eine Spule (L) und ein Plattenkondensator (C1) mit einem Plattenabstand
d1 = 4,8 mm verbunden sind, ist auf die Wellenlänge λ1 = 300 m abgestimmt. Wie muss der Abstand zwischen den Kondensatorplatten verändert werden, damit der Schwingkreis auf die Wellenlänge λ2 = 240 m abgestimmt ist?
12.Die Kapazität der Kondensatoren im Schwingkreis eines Radioempfängers kann von C1 = C bis C2 = 9C variieren. Bestimmen Sie den Wellenlängenbereich des Empfängers, wenn die minimale Kapazität C1 der Wellenlänge λ1 = 3 m entspricht.
(L1 = L2 = L)
13.Ein Schwingkreis mit der Kapazität C = 4 μF hat eine Frequenz f1 = 200 Hz. Wenn ein weiterer Kondensator mit der Kapazität Cx parallel zum Kondensator geschaltet wird, sinkt die Eigenfrequenz auf f2 = 100 Hz. Berechnen Sie die Kapazität des hinzugefügten Kondensators Cx.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
14.In einem Schwingkreis sind ein Kondensator (C = 0,01 μF), eine Spule (L = 0,1 H) und ein Widerstand (R = 1000 Ω) in Reihe geschaltet. Wie ist das Verhältnis der Frequenzen des Kreises mit Widerstand und ohne Widerstand?