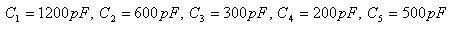Leiterkapazität
1.Erkläre den Begriff „Leiterkapazität“!
Lösung:
Kapazität eines Leiters ist die Fähigkeit eines Leiters, elektrische Ladung zu binden und zu verteilen.
Ladung im elektrischen Feld des Leiters
Spannung des Leiters
Kapazität eines Plattenkondensators:
Abstand zwischen den Platten, wirksame Fläche der Kondensatorplatten.
, Permittivität des Vakuums.
relative Permittivität des Mediums zwischen den Kondensatorplatten.
Kapazität einer Kugel:
Energie des elektrischen Feldes eines geladenen Kondensators:
Reihenschaltung von Kondensatoren:
Parallelschaltung von Kondensatoren:
2.Leite die Dimension der physikalischen Einheit Farad = F her. Zeige, dass gilt: C2·N−1·m−2 = F·m−1
Lösung:
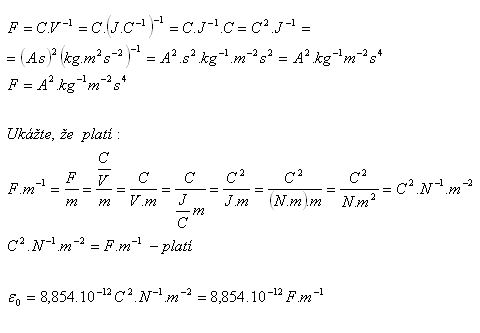
Damit ist gezeigt, dass 1 F = A2·kg−1·m−2·s4 und dass C2·N−1·m−2 = F·m−1 gilt.
3.Berechne die Kapazität eines Plattenkondensators, der aus 11 Platten mit den Abmessungen 3 cm und 2 cm besteht, wenn der Abstand zwischen den Platten 0,2 mm beträgt. Das Dielektrikum zwischen den Platten ist Glimmer mit εr = 6. Zwischen den 11 Platten befinden sich 10 Spalte.
Lösung:
Analyse:
S = a·b = 3 cm·2 cm = 6 cm2 = 6·10−4 m2, l = 2·10−4 m, εr = 6, ε0 = 8,854·10−12 C2·N−1·m2
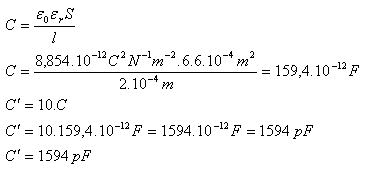
Die Kapazität des Kondensators beträgt C' = 1594 pF.
4.Wie groß ist die Spannung zwischen den Platten eines Luftkondensators mit zwei quadratischen Platten der Seitenlänge 10 cm, die durch 2 cm getrennt sind, wenn seine Ladung 8,854·10–3 μC beträgt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
5.Wie groß ist die Kapazität unserer Erde?
Bitte melden Sie sich an, um die Lösung anzuzeigen.6.Auf welches Potential wird ein Leiter mit einer Kapazität von 20 Pikofarad durch eine Ladung von 1 Mikrokoulomb aufgeladen?
Bitte melden Sie sich an, um die Lösung anzuzeigen.7. Bestimmen Sie die relative Permittivität des Dielektrikums in einem Plattenkondensator, dessen Platten mit einer Fläche von 1000 cm2 durch 0,1 mm getrennt sind und der mit einer Ladung von 17,7·10-6C auf 100 V aufgeladen ist.
Bitte melden Sie sich an, um die Lösung anzuzeigen.8. Kondensatoren mit Kapazitäten von 6·10-6F und 4·10-6F sind in Reihe geschaltet, und parallel zu ihnen ist ein Kondensator mit Kapazität 2·10-6F angeschlossen. Wie groß ist ihre resultierende Kapazität?
Bitte melden Sie sich an, um die Lösung anzuzeigen.9.Zwei Kondensatoren mit gleicher Kapazität sind a) in Reihe und b) parallel geschaltet. Der Unterschied zwischen den resultierenden Kapazitäten beider Schaltungen beträgt 3·10-6F. Bestimmen Sie die Kapazität jedes Kondensators.
Bitte melden Sie sich an, um die Lösung anzuzeigen.10. Welche Energie wird in einem Kondensator gespeichert, dessen Platten eine Fläche von 0,3 m2 und einen Plattenabstand von 1 mm haben, wenn wir ihn auf eine Spannung von 1000 V aufladen? Die relative Permittivität beträgt 20.
Bitte melden Sie sich an, um die Lösung anzuzeigen.11. Zwei Kondensatoren mit Kapazitäten 12·10–6F und 24·10–6F sind in Reihe an eine Gleichspannungsquelle von 30 V angeschlossen. Bestimmen Sie:
- a.) die resultierende Kapazität
- b.) die Ladungen auf den Platten der Kondensatoren
- c.) das Verhältnis der Spannungen an den einzelnen Kondensatoren.
12. Die Platten eines Kondensators sind 5 mm voneinander entfernt und haben eine Fläche von 2 m2. Die Platten befinden sich im Vakuum. Berechnen Sie:
- a.) die Ladung auf jeder Platte
- b.) die Flächenladungsdichte. Die Spannung am Kondensator beträgt 10 000 V.
13. Kondensatoren mit Kapazitäten C1 = 2·10-6F und C2 = 3·10-6F sind parallel geschaltet. Auf dem Kondensator mit Kapazität C1 befindet sich eine Ladung Q1 = 6·10-6C. Wie groß ist die Spannung und wie groß ist die Ladung auf dem zweiten Kondensator?
Bitte melden Sie sich an, um die Lösung anzuzeigen.14. Drei Kondensatoren mit Kapazitäten C1 = 2·10-6F, C2 = 3·10-6F, C3 = 6·10-6F sind in Reihe geschaltet. Wie groß ist die resultierende Kapazität dieser Schaltung? Wie groß ist die Spannung an jedem Kondensator, wenn die gesamte Batterie an eine Spannung von 200 V angeschlossen wird?
Bitte melden Sie sich an, um die Lösung anzuzeigen.15.Wie ändern sich a) die Kapazität des Kondensators und b) die Feldstärke, wenn wir Papier zwischen die Kondensatorplatten einfügen und den Zwischenraum vollständig ausfüllen?
Bitte melden Sie sich an, um die Lösung anzuzeigen.16. Der Abstand zwischen den Platten eines Plattenkondensators beträgt 8,854 mm, die Flächenladungsdichte auf den Platten ist 10 nC·m–2. Zwischen den Platten befindet sich Luft. Wie groß ist die Spannung zwischen den Platten?
Bitte melden Sie sich an, um die Lösung anzuzeigen.17.Die Kapazität der Erde beträgt 709,26·10-6F. Die Spannung zwischen einer nahegelegenen Wolke und der Erde erreichte im Moment des Blitzes einen Wert von 109V. Wie viel elektrische Energie wurde beim Blitz freigesetzt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.18.Ein Leidener Flasche mit Radius 5 cm und Höhe 20 cm besitzt eine Glaswandstärke von 3 mm. Die relative Permittivität des Glases beträgt 6. Berechnen Sie:
- a.) die Kapazität der Flasche
- b.) die Arbeit, die zum Aufladen der Flasche auf 30 000 V erforderlich ist
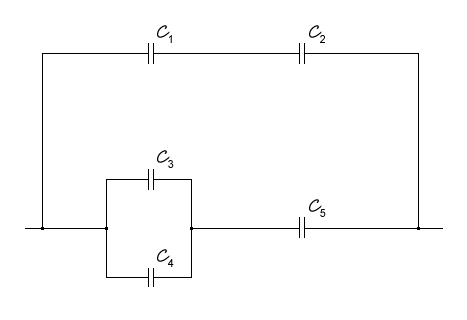
19. Bestimmen Sie die resultierende Kapazität der Kondensatoren (Diagramm), wenn Folgendes gilt:
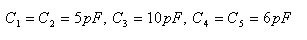
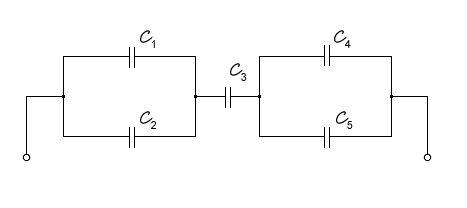
20.Berechnen Sie die resultierende Kapazität der Kondensatoren, die wie im Diagramm verbunden sind.