Starrer Körper
1.Was wissen wir über die Eigenschaften eines starren Körpers?
Lösung:
Ein starrer Körper ist ein ideales Objekt, dessen Form und Volumen sich unter der Einwirkung äußerer Kräfte nicht ändern. Äußere Kräfte bewirken eine Änderung des Bewegungszustands des starren Körpers. Die Bewegung des Körpers kann sein:
a.) Translationsbewegung
b.) Rotationsbewegung eines starren Körpers um eine Achse ist eine Bewegung, bei der jeder Punkt des Körpers zur selben Zeit die gleiche Winkelgeschwindigkeit hat.
Die Drehwirkung einer Kraft auf einen starren Körper wird durch das Drehmoment ausgedrückt:
F ist die angreifende Kraft, ist der Hebelarm. Der Hebelarm ist der Abstand der Wirkungslinie der Kraft von der Drehachse des Körpers.
Momentensatz: Die Drehwirkungen der auf einen starren Körper wirkenden Kräfte heben sich auf, wenn gilt:
Trägheitsmoment ist ein Maß für den Widerstand eines Körpers gegen die Rotationsbewegung:
Kinetische Energie eines rotierenden Körpers:
2.An den Ecken einer rechteckigen Platte mit den Seiten a = 30 cm, b = 40 cm wirken Kräfte F1 = 10 N, F2 = 20 N, F3 = 30 N, F4 = 40 N. Die Platte kann sich um eine zur Platte senkrechte Achse drehen, die durch den Eckpunkt A geht. Wie groß ist das resultierende Moment der auf die Platte wirkenden Kräfte?
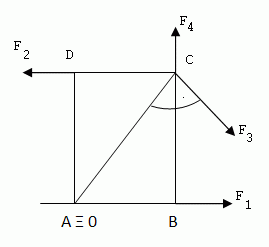
Lösung:
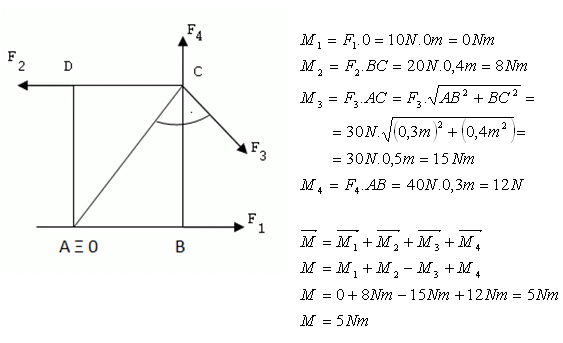
Das resultierende Moment der Kräfte beträgt 5 N·m.
3.Eine rechteckige Platte mit den Abmessungen a = 20 cm, b = 10 cm ist so gelagert, dass sie sich um eine durch ihr Zentrum O gehende, zur Platte senkrechte Achse drehen kann. Kraft F1 = 800 N. Berechne den Betrag der Kraft F2, damit die Platte in Ruhe bleibt.
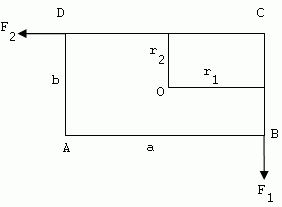
Lösung:
Analyse:
a = 20 cm = 0.2 m, b = 10 cm = 0.1 m, r1 = 0.1 m, r2 = 0.05 m, F1 = 800 N
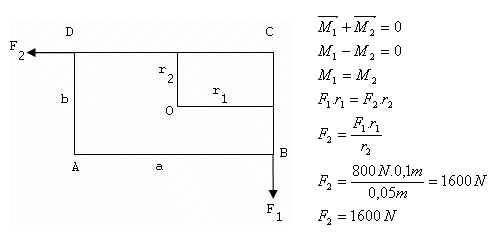
Damit die Platte in Ruhe bleibt, muss die Kraft F2 gleich 1600 N sein.
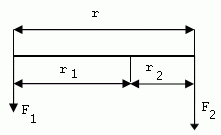
4.Der Stab ist 1,2 m lang. An seinen Enden hängen Gewichte mit den Massen 5 kg und 7 kg. Wo muss der Stab abgestützt werden, damit er im Gleichgewicht bleibt?
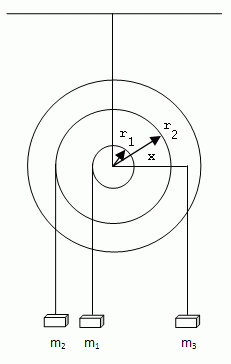
5.An einer rotierenden Scheibe sind auf derselben Seite der Drehachse Gewichte mit m1 = 0.5 kg im Abstand r1 = 0.2 m und m2 = 0.2 kg im Abstand r2 = 0.4 m aufgehängt. In welchem Abstand von der Achse muss auf der anderen Seite ein Gewicht m3 = 0.6 kg aufgehängt werden, damit Gleichgewicht entsteht?
6.Wie viel Arbeit müssen wir verrichten, um einen Stahlzylinder mit der Masse 800 kg und dem Grundkreisradius 0.5 m auf 48 Umdrehungen pro Minute hochzudrehen? Trägheitsmoment eines Vollzylinders: (Tabellen)
Bitte melden Sie sich an, um die Lösung anzuzeigen.
7.Wie groß ist das Trägheitsmoment eines Schwungrads, wenn bei der Bremsung durch Arbeit von 1260 J seine Drehzahl von 320 min-1 auf 254 min-1 abfällt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
8.Eine Stahlscheibe wurde mit einem Seil der Länge 80 cm angetrieben, an dem eine Kraft von 30 N wirkte. Wie viele Umdrehungen macht sie in 1 Sekunde, wenn ihr Trägheitsmoment 0.03 kg·m2 beträgt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
9.Auf welche Höhe würde ein Spielzeugauto einen Hügel hinauffahren, wenn es nur von einem Schwungrad mit dem Trägheitsmoment 0.1 kg·m2 angetrieben wird? Das Schwungrad macht 4 Umdrehungen pro Sekunde. Die Masse des Spielzeugautos beträgt 8 kg.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
10.Bestimme die Mindestfrequenz, die ein Schwungrad mit dem Trägheitsmoment 305 kg·m2 erreichen muss, damit es über eine Zeit von 10 Minuten eine Leistung von 25 kW abgibt.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
11.
Erläutere, wann wir den Satz von Steiner (Parallelachsen-Satz) bei der Berechnung des Trägheitsmoments eines starren Körpers verwenden?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
12.Berechne das Trägheitsmoment einer massiven homogenen Kugel mit Radius r = 10 cm und Masse 25 kg bezüglich einer Achse, die die Kugeloberfläche tangiert.
13. Bestimme die Länge des Stabs l mit der Masse 1.2 kg und dem Trägheitsmoment 0.592 kg·m2, wenn der Stab im Abstand 0.4 m von der festen Achse rotiert.
Bitte melden Sie sich an, um die Lösung anzuzeigen.
14.Ein Vollrad (Kreisscheibe) mit der Masse 20 kg und dem Radius r = 50 cm rollt mit der Geschwindigkeit 10 m·s-1. Wie groß ist seine kinetische Energie?
Bitte melden Sie sich an, um die Lösung anzuzeigen.
15.
Welche Geschwindigkeit erhält eine Kugel, wenn sie eine schiefe Ebene aus einer Höhe von 1 m hinunterrollt?
Bitte melden Sie sich an, um die Lösung anzuzeigen.