Quantenoptik

1. Was ist ein Photon?

Lösung:

Theorien über die Natur des Lichts:

a.) Licht ist eine mechanische Welle des Äthers. (Huygens, Young)
b.) Licht ist ein Strom von Teilchen (Korpuskeln), die von der Quelle emittiert werden. (Newton)
c.) Licht ist eine elektromagnetische Welle mit einer Frequenz von etwa 3.8·10¹⁴ Hz bis 7.8·10¹⁴ Hz, die sich kontinuierlich von der Quelle aus ausbreitet. (Maxwell)
d.) Die Energie der Strahlung (des Lichts) ist nicht kontinuierlich im Raum verteilt, sondern besteht aus einer bestimmten Anzahl diskreter Energiepakete (Quanten), die nur als ganze Einheiten emittiert und absorbiert werden können. Ein Strahlungsquant (Lichtquant) wird Photon genannt. (Planck, Einstein)

Jedes Photon hat:
Energie: E=h⋅f=m⋅c2=p⋅ch=6.625⋅10−34 J⋅sc=3.108 m⋅s−1E = h \cdot f = m \cdot c^2 = p \cdot c \quad h = 6.625 \cdot 10^{-34} \, J \cdot s \quad c = 3.10^8 \, m \cdot s^{-1}
Impuls p=m⋅c=h/λp = m \cdot c = h / \lambda

Wellen–Teilchen-Dualismus:
de Broglie: Jedes bewegte Teilchen mit Masse mm und Geschwindigkeit vv besitzt ebenfalls eine Welle mit der Wellenlänge

λ=hm⋅v\lambda = \frac{h}{m \cdot v}

Compton: Jedes Photon kann als massives Teilchen mit Ruhemasse null betrachtet werden, das nur mit der Geschwindigkeit cc existiert.

Compton-Experiment:

E=h⋅(f1−f2)E = h \cdot (f_1 - f_2)

Δλ=hme⋅c(1−cos⁡ϑ)ϑ= Ablenkwinkel des Photons 

Photoelektrischer Effekt (Photoemission) ist die Freisetzung von Elektronen aus Metallen durch einfallende Strahlung (Photonen):

  • intern (Elektronen werden aus Atomen emittiert, bleiben aber im Metall)

  • extern (Elektronen werden von der Oberfläche des Metalls emittiert und bewegen sich mit Geschwindigkeit vv im Raum)

Einsteins Gleichung der Photoemission:

hf=We+12meve2h f = W_e + \frac{1}{2} m_e v_e^2

hf=kf0h f = k f_0

We=Austrittsarbeitf0=GrenzfrequenzW_e = \text{work function} \quad f_0 = \text{threshold frequency}

hf=U⋅eh f = U \cdot e

U=Spannunge=1.602⋅10−19 CU = \text{voltage} \quad e = 1.602 \cdot 10^{-19} \, \text{C}

Franck–Hertz-Experiment zeigt, dass Atome Energie in Quanten absorbieren.

 

2. Berechnen Sie die Energie eines Photons, das den Extremwerten des sichtbaren Lichts entspricht. Violett hat eine Wellenlänge λV=390 nm, Rot λR=790 nm. Geben Sie das Ergebnis in Joule und in eV an. 1eV=1.602·10-19J.

Lösung:

Analyse:

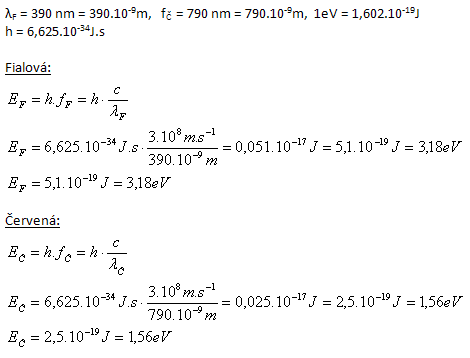
 physics-quantum-optics-2.gif

Ein Photon violetten Lichts hat eine Energie von 3.18 eV, ein Photon roten Lichts 1.56 eV.

3. Vergleichen Sie die Energie eines Photons gelben monochromatischen Lichts (λ = 500·10-9m) mit der mittleren kinetischen Energie eines Moleküls eines idealen Gases in seiner ungeordneten Bewegung bei einer Temperatur von 00C.

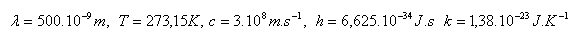
physics-quantum-optics-3z.gif

Lösung:

Analyse:

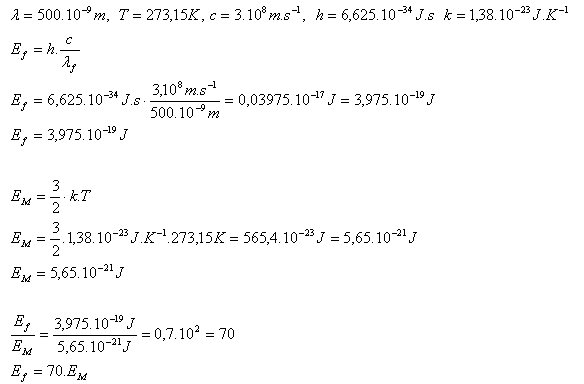
physics-quantum-optics-3r.gif

Die Energie eines Photons gelben Lichts ist 70-mal größer als die Energie eines Moleküls eines idealen Gases bei 00C.

4.Das menschliche Auge kann Licht wahrnehmen, wenn die Leistung der auf das Auge fallenden Lichtstrahlung mindestens P=2·10-17W beträgt. Bestimmen Sie, wie viele Photonen mit Wellenlänge λ = 500·10-9m in 1 Sekunde auf das Auge treffen.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

5.Welche Grenzfrequenz der elektromagnetischen Strahlung ist notwendig, um die Oberfläche von Nickel zu bestrahlen, sodass der äußere photoelektrische Effekt auftritt? Die Austrittsarbeit der Elektronen aus Nickel beträgt 5 eV.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

6.Bestimmen Sie, ob Photoemission auftreten kann, wenn Licht mit einer Wellenlänge von λ = 390·10-9m auf Zink fällt.

Die Austrittsarbeit für Zink ist We = 4eV, λ = 390nm,  We = 4eV = 4·1.602·10-19J = 6.408·10-19J,  λ0 = ?
Bitte melden Sie sich an, um die Lösung anzuzeigen.

7.Mit welcher Geschwindigkeit verlassen Elektronen eine Platinplatte (f0 = 12.8·1014Hz), wenn ultraviolettes Licht mit der Wellenlänge λ = 150nm auf sie fällt? (me = 9.1·10-31kg)

Bitte melden Sie sich an, um die Lösung anzuzeigen.

8.Die de-Broglie-Wellenlänge eines beschleunigten Elektrons beträgt λ = 3.87·10-11m. Das Elektron wurde aus der Ruhe in einem elektrischen Feld mit der Spannung U beschleunigt. Berechnen Sie:

  • a) die Geschwindigkeit des Elektrons
  • b) die Beschleunigungsspannung
Bitte melden Sie sich an, um die Lösung anzuzeigen.

9.Ein Photon ultravioletter Strahlung hat eine Wellenlänge von λ = 100nm. Berechnen Sie

  • a) wie viele Photonen einer Energie von 1J entsprechen
  • b) wie viele Photonen einer Masse von 1 Mikrogramm entsprechen
Bitte melden Sie sich an, um die Lösung anzuzeigen.

10.Im Compton-Experiment hat das einfallende Photon die Frequenz f1=1.5·1020Hz, das Photon nach dem Stoß hat die Frequenz f2=1.1·1020Hz.

  • a) Bestimmen Sie die Energie, die das Elektron, das mit dem Photon wechselwirkte, gewinnt. Geben Sie die Energie in eV an.
  • b) Bestimmen Sie die Änderung der Wellenlänge des Photons.
Bitte melden Sie sich an, um die Lösung anzuzeigen.

11.Im Franck–Hertz-Experiment stellten die Autoren fest, dass der Stromabfall bei einer Spannung im elektrischen Feld auftritt, das die Elektronen beschleunigt, die gleich U = 4.9V ist, und dass Quecksilberdämpfe Strahlung mit der Wellenlänge λ = 253.2nm emittieren. Berechnen Sie den Wert des Planckschen Wirkungsquantums h.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

12.Beim Compton-Effekt der Streuung von Photonen an einem Elektron ändert sich die Wellenlänge des Photons um Δλ=4.85·10–12m. Um welchen Winkel υ weicht das Photon von der ursprünglichen Richtung ab?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

13.Eine Röntgenröhre arbeitet mit einer Spannung von 20 kV, einem Strom von 10 mA und einem Wirkungsgrad von η = 0.2%. Berechnen Sie:

  • a.) die kurzwellige Grenze des kontinuierlichen Spektrums
  • b.) die in Form von Röntgenstrahlung abgestrahlte Leistung
Bitte melden Sie sich an, um die Lösung anzuzeigen.

14.Auf einem Bildschirm eines Fernsehempfängers werden Elektronen durch eine Potentialdifferenz von 15 kV beschleunigt. Wie groß sind die Geschwindigkeit und die de-Broglie-Wellenlänge dieser Elektronen?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

15.In einem Elektronenmikroskop werden Elektronen mit einer Spannung von 105 V emittiert. Wie groß ist das Auflösungsvermögen λ dieses Mikroskops?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

16.Wie groß ist die Energie eines Neutrons, dessen Wellenlänge in der Größenordnung des Abstands zwischen Atomen in einem Kristallgitter
(10–10 m) liegt?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

17.Wie viele Photonen roten Lichts ( λ = 750 nm ) werden benötigt, um eine kleine Kugel mit einer Masse von
3 Mikrogramm zu erzeugen?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

18.Eine Glühbirne emittiert sichtbares Licht mit der Frequenz 5·1014 Hz. Wie groß sind die Energie und die Masse eines Photons?

Bitte melden Sie sich an, um die Lösung anzuzeigen.

19.Vergleichen Sie die de-Broglie-Wellenlängen eines Elektrons und eines Protons, die sich mit derselben Geschwindigkeit bewegen.

Bitte melden Sie sich an, um die Lösung anzuzeigen.

20.Ein Helium–Neon-Laser ist eine Quelle monochromatischer Strahlung mit der Wellenlänge 632.8 nm. Seine Leistung beträgt 2 mW. Bestimmen Sie die Energie und die Masse der Photonen der Laserstrahlung. Wie viele Photonen werden pro 1 Sekunde emittiert?

Bitte melden Sie sich an, um die Lösung anzuzeigen.