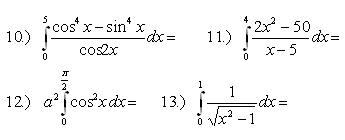Definite integral - Leibnitz and Newton's method

1.What are the properties of a definite integral?

Solution:

Leibniz–Newton formula:

Let f(x) be a continuous function on the interval <a,b>, (where a is the lower bound and b is the upper bound of the interval). Then the Leibniz–Newton formula applies:


∫abf(x) dx=[F(x)]ab=F(b)−F(a),a<b\int_a^b f(x)\,dx = \big[F(x)\big]_a^b = F(b) - F(a), \quad a < 

Properties:

1.)

∫abf(x) dx=−∫baf(x) dx\int_a^b f(x)\,dx = -\int_b^a f(x)\,dx

2.)

∫abf(x) dx=∫acf(x) dx+∫cbf(x) dx,a<c<b\int_a^b f(x)\,dx = \int_a^c f(x)\,dx + \int_c^b f(x)\,dx, \quad a < c < b


2.Calculate the integrals:

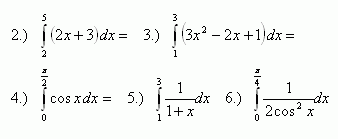
urcity-integral-leibniz–newtonova-metoda-2.gif 

Solution:

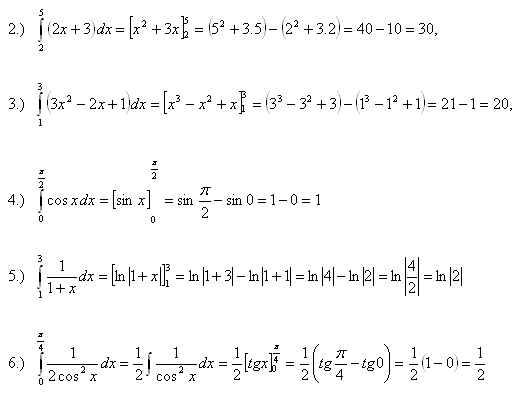
urcity-integral-leibniz–newtonova-metoda-2.gif 

3.Calculate the integrals:

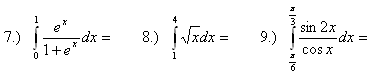
urcity-integral-leibniz–newtonova-metoda-3z

Solution:

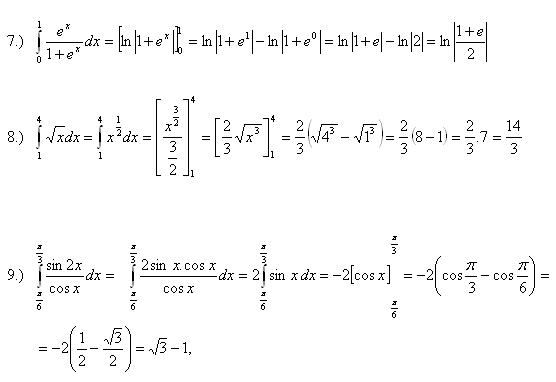
urcity-integral-leibniz–newtonova-metoda-3r  

4.Calculate the integrals:

urcity-integral-leibniz–newtonova-metoda-4z
Please log in to view the solution.