Combinations

1. Characterize combinations and combinations with repetition.

Solution:

a) k-combinations from a set with n elements (without repetition) 
k-combinations from a set of n elements (without repetition) is an unordered collection of k distinct elements taken from a given set.


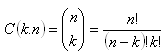
b) k-combinations from a set with n elements (with repetition) 
k-combinations from a set of n elements (without repetition) is an unordered collection of k not necessarily distinct elements taken from a given set.

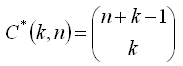
2. On the plane there are 6 different points (no 3 of them are lying on the same line). How many segments do you get by joining all the points?

Solution:


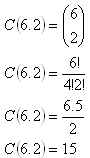
You get 15 different segments.

3.On a circle there are 9 points selected. How many triangles with edges in these points exist?

Solution:


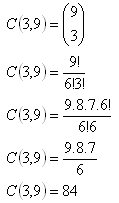
There are 84 such triangles.

4.a) Find out a formula for counting the number of diagonals in a convex n-gon!
b) How many diagonals has a 10-gon?

5. In how many ways you can choose 8 of 32 playing cards not considering their order?

6.A teacher has prepared 20 arithmetics tasks and 30 geometry tasks. For a test he‘d like to use:

7.On a graduation party the graduants pinged their glasses. There were 253 pings. How many graduants came to the party?

8.If the number of elements would raise by 8, number of combinations with k=2 without repetition would raise 11 times. How many elements are there?

9. For which x positive integer stands:

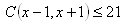
10.Two groups consist of 26 elements and 160 combinations without repetition for k=2 together. How many elements are in the first and how many in the second group?

11. In the confectioners 5 different icecreams are sold. A father would like to buy 15 caps of icecream for his family. In how many ways can he buy the icecream?

12.From how many elements 15 combinations with repetition (k=2) can be made?

Register and unlock all the solutions!

You will find a lot of exercises, sample solutions and useful materials on priklady.eu.
Registered users can see all the content – without restrictions!
Just log in and start learning effectively.

Register now and start learning!

Already have an account? Log in