Permutations (general)

1.Define and characterize permutations and permutations with repetition.

Solution:

Permutations

A permutation is an ordered sequence of k elements selected from a given finite set of n numbers, without repetitions, and not necessarily using all n elements of the given set. 

Number of possible permutations: 

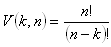
variacie1

Permutations with repetition

A permutation is an ordered sequence of k elements selected from a given finite set of n numbers, with repetitions, and not necessarily using all n elements of the given set. 

Number of possible permutations with repetition:

V*(k,n) = nk

2. From a given set M = {a,b,c,d} enumerate the permutations with and without repetition for k=2. Determine their number.

Solution:

a) Permutations:

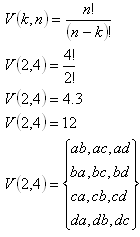
variacie2a

b) Permutations with repetition:

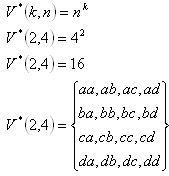
variacie2b

3. There are 7 members in a committee. How many ways are there to choose a chairman, deputy chairman, secretary and a cash keeper?

Solution:
Permutations, n = 7, k = 4
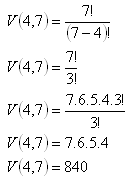
variacie3
There are 840 ways of choosing the four officials.

4.Eight students promissed to send a postcard each other. How many postcards did they send together?

Please log in to view the solution.

5.From how many numbers 240 permutations can be made if the number of elements to be selected is 2?

Please log in to view the solution.

6.If the number of members increments by 2, the number of possible variations with k=3 increments by 384. How many members are there?

Please log in to view the solution.

7. You have 6 different tickets in your pocket marked with numbers 1-6. How many ways are there to choose 3 of them (considering the order), if
a) the selected ticket is not returned to the pocket.
b) the selected ticket is returned to the pocket.

Please log in to view the solution.

8.Number of permutations without repetition with k=3 from x members is lower than number of permutations with repetition with k=3 from x members by 225. How many members are there?

Please log in to view the solution.