Function features

1. What do you remember about the properties of functions?

Solution:

A function f of a real variable x is a rule that assigns to each x ∈ R at most one y ∈ R such that
y = f(x)

The domain of the function D is the set of all x ∈ R for which there exists exactly one y ∈ R such that
y = f(x).

The range of the function H is the set of all y ∈ R for which there exists at least one x ∈ R such that
y = f(x).

, the function is increasing
x2>x1,f(x2)<f(x1)x_2 > x_1, f(x_2) < f(x_1), the function is decreasing
x2>x1,f(x2)≤f(x1)x_2 > x_1, f(x_2) \leq f(x_1), the function is non-increasing
x2>x1,f(x2)≥f(x1)x_2 > x_1, f(x_2) \geq f(x_1), the function is non-decreasing
x2≠x1,f(x2)≠f(x1)x_2 \neq x_1, f(x_2) \neq f(x_1), the function is injective

If there exists h∈, such that f(x)≤h, the function is bounded from above
If there exists d∈R, such that f(x)≥df(x) \g, the function is bounded from below
If the function is bounded from above and from below, it is bounded

If f(x+kp)=f(x)f(x + kp) = f(x), the function is periodic (p=p = period)
If f(−x)=f, the function is even
If f(−x)=−f(x)f(-x) = -f(x), the function is odd

A function f(x)f(x) has an inverse function f−1(x)f^{-1}(x). It holds:
D−=H, H−=D

 

 

Two functions are equal: f(x) = g(x) if: D(f) = D(g)

                                                       f(x) = g(x)

 

Which of the following graphs represent functions?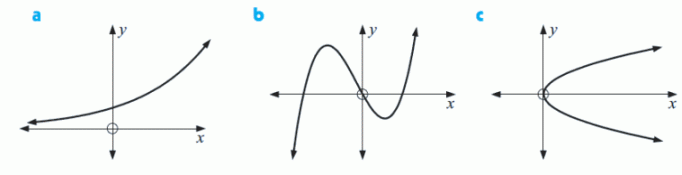
properties-of-functions-1az

 

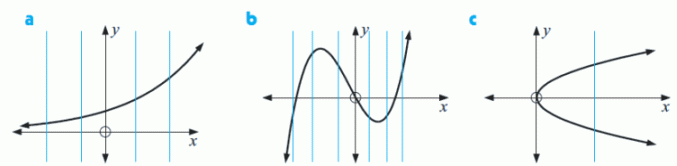
properties-of-functions-1ar

Function                                                  Function                                         Not a function 

2.Determine whether the following expressions are functions:

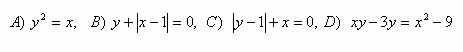
properties-of-functions-2z

Solution:

function-2-r 

3.Decide whether the following functions are equal:

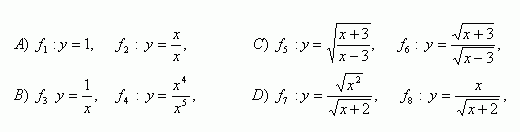
properties-of-functions-3z

Solution:

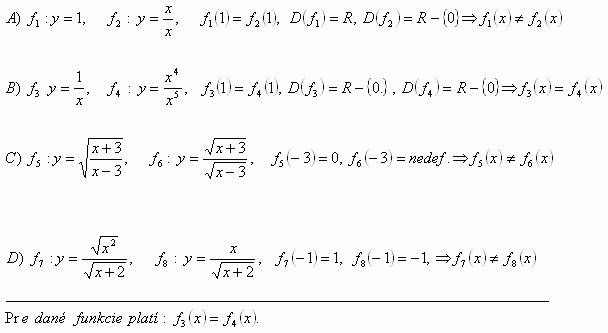
properties-of-functions-3r

For the given functions apply: f3(x) = F4(X)

4.Determine the evenness or oddness of the functions:

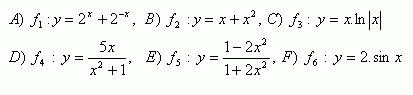
properties-of-functions-4z
Please log in to view the solution.

5. Determine which of the following functions are bounded in the given domain.

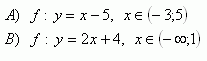
properties-of-functions-5z
Please log in to view the solution.

6. For the given functions, create inverse functions.

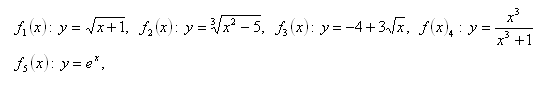
properties-of-functions-6z
Please log in to view the solution.

7. Determine the inverse function for the functions:

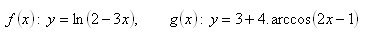
properties-of-functions-7z
Please log in to view the solution.

8. In the function f(x): y = ax2 + bx + c , x ∈ R, determine a, b, c ∈ R such that f(0) = -3, f(-1) = -6, f(2) = 15.

Please log in to view the solution.

9. Determine b, d of the function f: y = (x + b):(x + d) such that f(1) = -1,  f(-1) = -1/3

Please log in to view the solution.

10.Determine the set of all functions f(x) for which the following holds:

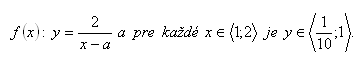
properties-of-functions-10z
Please log in to view the solution.

11.The function f: y= -2x +3 is given

a.) Determine f(0),  f(-5)
b.) For which x is f(x) = 1,  f(x) = -5
c.) Determine the intersection of the graph of the function with the coordinate axes
Please log in to view the solution.

12.Write a linear function whose graph passes through the points

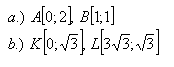
properties-of-functions-12z
Please log in to view the solution.

13.According to the car manufacturer, the fuel consumption of a car per 100 km is as follows. At a speed of 80 km/h it consumes 6 liters of fuel, at a speed of 110 km/h it consumes 8.1 liters. Determine the car’s consumption at a speed of 90 km/h.

Please log in to view the solution.

14.The function f: y = x2 - 4x -12 is given.

a.) Determine for which x it holds that f(x) = 9
b.) Determine the intersections of the graph of the function with the coordinate axes
Please log in to view the solution.

15.Write a quadratic function whose elements are the ordered pairs

A[0;1], B[2;-1], C[1;-1]
Please log in to view the solution.

16.The quadratic function f: y = x2 – 3x + c is given. Determine c such that the function

a.) has no common point with the x-axis
b.) has exactly one common point with the x-axis
c.) has exactly two common points with the x-axis
Please log in to view the solution.

17.The quadratic function f: y = x2 + 4x – 5 is given. Determine its intersections with the coordinate axes and the vertex of its parabolic graph.

Please log in to view the solution.

18.Determine the coefficients a, b so that the graph of the function f: y = a·log x + b passes through points K, L given that:

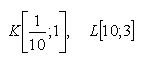
vlastnosti-funkcii-18z.gif
Please log in to view the solution.

19.Determine the coefficients a, b so that the function f: y = a2x + b passes through the origin of the coordinate system and the point M [1; 1].

Please log in to view the solution.

20.For which real numbers x do the functions f(x) = (5!)x and g(x) = (4!)x+1 attain the same values?

Please log in to view the solution.