Cube, Cuboid, Prism and Cylinder

1. State the basic formulas for calculating volume and surface area:

Solution:

Cube

a – edge of the cube

volume V = a³

surface area S = 6a²



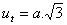
Cuboid

a, b, c – edges of the cuboid

volume V = a·b·c

surface area S = 2(ab+ac+bc)



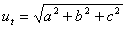
Prism

S_p – area of the base
Q – lateral area
v – height of the prism

volume V = S_p·v

surface area S = 2S_p + Q

Cylinder

r – radius of the base
v – height of the cylinder

volume V = π·r²·v

surface area S = 2πr(r+v)

Q = 2πrv

2. Two cube-shaped crates with edges a = 70 cm, b = 90 cm are to be replaced by one cube-shaped crate.

Solution:



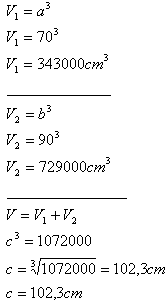
The edge of the replacement cube will be c = 102.3 cm.

3. The edge of the second cube is 2 cm larger than the edge of the first cube. The difference of the cubes’ volumes is 728 cm³.

Solution:

Edge of the first cube: x
Edge of the second cube: x + 2



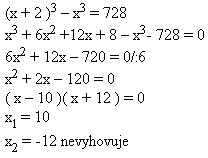
The edge of the first cube is 10 cm, of the second 12 cm.

4. A cube with edge a is given. Known values are in the table.

Complete the table!

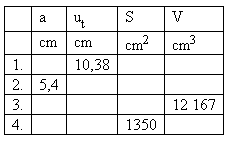
5. The edges of two cubes differ by 22 cm. Their surface areas differ by 19,272 cm².

6. A cuboid has dimensions a = 4 cm, b = 3 cm, c = 5 cm.

7. The surface area of a cuboid is S = 376 cm². Its edges are in the ratio a:b:c = 3:4:5.

8. A water tank in the shape of a cuboid contains 1500 hl of water; the water height is 2.5 m.

9. Calculate the volume of a cuboid if its base has S₁ = 272 cm² and the lateral faces have S₂ = 240 cm², S₃ = 255 cm².

10. What is the mass of an iron rod (ρ = 7800 kg·m^-3) that is 1.5 meters long and has a square cross-section with side a = 45 mm?

11. The base of a right triangular prism is a right triangle with legs a = 9 cm, b = 12 cm. The height of the prism is twice the hypotenuse of the right-angled base.

12. How much soil must be moved when digging a straight trench 170 m long, whose cross-section is an isosceles trapezoid with bases a = 150 cm, c = 80 cm and height v = 83 cm?

13. Calculate the volume and surface area of a prism whose base is a rhombus with diagonals u₁ = 12 cm, u₂ = 16 cm. The height of the prism equals twice the base edge.

14. The table lists quantities characterizing various cylinders.

Complete the table!

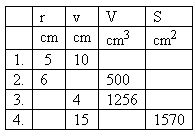
15. The lateral surface of a right circular cylinder, developed into a plane, is a square with area a² = 81 cm².

16. An equilateral cylinder (v = 2r) has volume V = 250 cm³.

17. An aluminum wire (ρ = 2.7 g·cm^-3) with diameter d = 3 mm has total mass m = 1.909 kg.

18. The outer circumference of a brass tube (ρ = 8.5 g·cm^-3) is 31.4 cm. Its mass is 3.14 kg and its length is 60 cm.

Register and unlock all the solutions!

You will find a lot of exercises, sample solutions and useful materials on priklady.eu.
Registered users can see all the content – without restrictions!
Just log in and start learning effectively.

Register now and start learning!

Already have an account? Log in