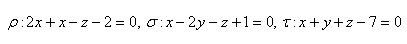Point, line, and plane
1. Explain in which mutual positions the following can be:
a) a point and a plane
b) a line and a plane
Solution:
Point and plane.
Point A[a1; a2; a3] lies in plane ρ: a.x + by + cz + d = 0 if its coordinates satisfy the equation of plane ρ.
Point A[a1; a2; a3] does not lie in plane ρ: ax + by + cz + d = 0 if its coordinates do not satisfy the equation of plane ρ.
The distance of point A[a1; a2; a3] from plane ρ: ax + by + cz + d = 0 is given by:
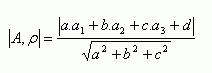
Line and plane.

2. Which of the points A [3;2;7], B[0;2;1], C[-8;-2;-1] lie in plane τ : 2x – 3y – 2z + 8 = 0. What must the value of x be so that point M[x;-6;2] also lies in the given plane?
Solution:
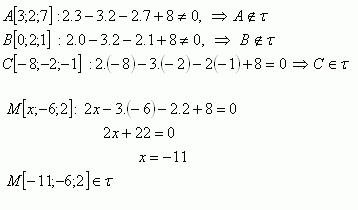
The points C [-8;-2;-1] and M [-11;-6;2] lie in plane τ.
3. Determine whether point A[9;-2;0] lies in plane ξ: 3x + 2y – 6z + 26 = 0. If it does not lie in it, calculate its distance from the given plane.
Solution:
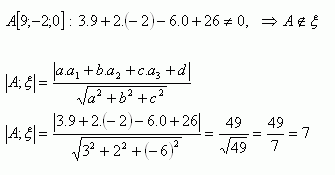
Point A does not lie in plane ξ. Its distance from this plane is 7 units.
4. Calculate the distance from the origin of the coordinate system to the plane:
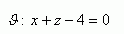
5. Determine the mutual position of planes ρ and τ. If they are parallel and distinct, also find their distance. The equations of the planes are:

6. What must hold for the y-coordinate of point A [1;y;0] so that its distance from plane τ: 3x – 2y – 6z = 0 is 5 units?
Please log in to view the solution.
7. Determine the mutual position and the intersection point of the line and the plane, if they are not parallel.
τ: x + y + z + 1
Line:
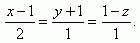
8. Given is line p and plane ρ. Find their common point and the angle between the line and the plane. Their equations are:
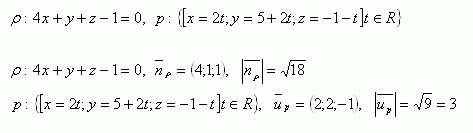
9. Determine the mutual position of planes ρ and π, whose equations are:
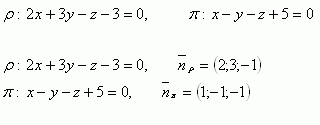
10. Calculate the angle between two non-parallel planes:
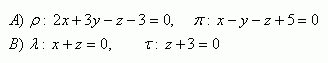
11. Determine the common point of line p and plane τ if:
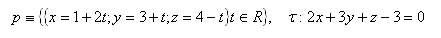
12.The distance of point A from plane σ represents the side of square ABCD. Calculate the area of this square if:
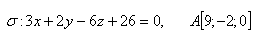
13. Calculate the distance of two parallel planes σ and τ if:
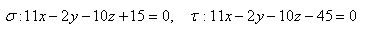
14. Calculate the length of the altitude drawn from vertex V in tetrahedron ABCV, if:
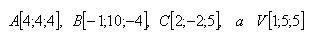
15. Determine real numbers a, b so that planes π and τ are parallel, given that:
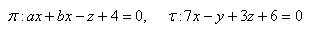
16. Determine the mutual position of planes σ and η if:
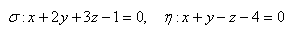
17. Show that the coordinate planes xy and yz are perpendicular to each other.
Please log in to view the solution.18. Determine the angle between line p and plane μ if:
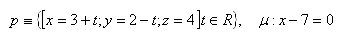
19.The vertices of the tetrahedron are points A, B, C, D. Determine the angle between edge AD and plane ρ = ABC if:
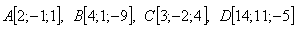
20. Determine the mutual position of three planes if: