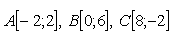Vector in a plane
1.Characterize the properties of a vector in a plane:

2.Given are points A[-2;5], B[1;yB], and C[4;-3]. Determine B so that the following holds true:
b) vectors AB and AC are parallel
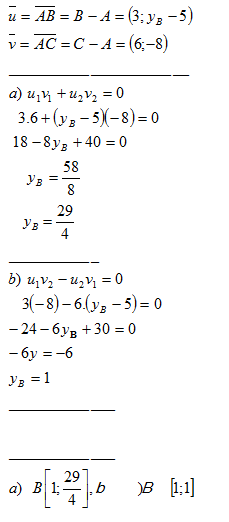
3.Given is vector v = AB as follows: A[1;1], B[b1;b2] and the center of the vector S[4;5].
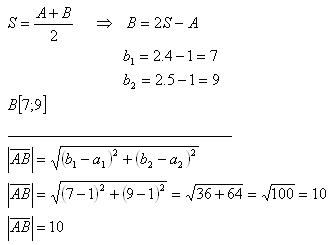
Point B has coordinates B[7;9]. The magnitude of the vector is 10 units.
4.The points A[2;-3] and B[x;0] are given.
5.Prove that the triangle whose vertices are points A[-3;-2], B[1;4], and C[-5;0] is isosceles.
Please log in to view the solution.6.Given are vectors a = (3;-2) and b = (-1;5).
a.c = 17
b.c = 3
7.Find the vector v, perpendicular to the vector u = (3;4) and whose magnitude is 15.
Please log in to view the solution.8.The vertices of the triangle ΔABC are the points A[1;1], B[2;-1] and C[3;2].
9.On the coordinate axes, find the point that is 5 from point A [4;-6].
Please log in to view the solution.10.The vertices of the quadrilateral are at points: A[0;0], B[3;-4], C[6;0] and D[3;4].
11.Points A, B, C are the vertices of triangle ABC. Show that triangle ABC is equilateral. Calculate its area.
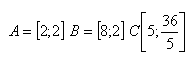
12.Points A, B, C are the vertices of triangle ABC. Mark the midpoints of sides AC, BC as M,N. Show that the midpoint MN is parallel to side AB and that MN = 0.5AB.
13.Given isosceles trapezoid ABCD with vertices
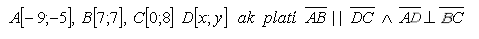
Determine the coordinates of point D.
14.Determine the coordinates of the center S and the size of the radius r of the circle that passes through the points A,B,C. Solve for the points:
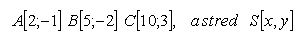
15.Find the coordinates of the center of gravity of a system of four bodies of equal mass, which lie at points A,B,C,D. The center of gravity T is the center of the line segment, whose endpoints are at the center of the vectors
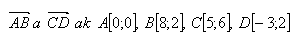
16.Point A [2;5] is the origin of the force F, whose projection on the coordinate axes is x = 3; y = 3. Calculate the end of the vector that represents the force F.
17.Given are three points A,B,
- a.) Prove that they lie on the same line
- b.) Find the ratio of the magnitudes of the vectors
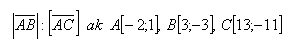
18.An isosceles triangle ABC has base AB with vertex A and base center S. Its vertex C lies on the x-axis. Determine the vertices of the triangle B and C.
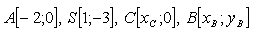
19.Given a vector u = (5 ;-3) and a vector v = (1;yv) such that
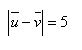
Determine yv
20.Points A,B,C are the vertices of triangle ABC and points M,N,P are the midpoints of the sides of this triangle. Determine the coordinates of three vectors whose positions coincide with the medians of triangle ABC such that the starting point is always at the vertex of the triangle. Calculate the magnitudes of these vectors.