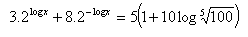Logarithmic Exponential Equations
1. Solve:
log3(2x - 7) = 2 2x > 7
Solution:
log3(2x - 7) = 2
log3(2x - 7) = log332
2x – 7 = 32
2x – 7 = 9
2x = 16
2x = 24
x = 4
K = {4}
log3(2x - 7) = 2
log3(2x - 7) = log332
2x – 7 = 32
2x – 7 = 9
2x = 16
2x = 24
x = 4
K = {4}
2. Solve:
log2( 9- 2x) = 3 – x 2x < 9
Solution:
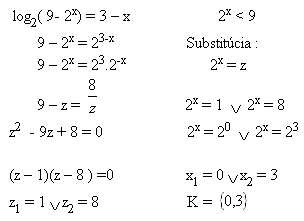
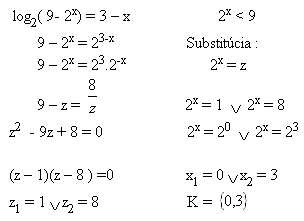
3. Solve:
log3( 1 + log3(2x-7)) = 1 2x > 7
Solution:
log3( 1 + log3(2x-7)) = 1
log3( 1+ log3(2x-7)) = log33
1 + log3(2x-7) = 3
log3(2x-7) = 2
log3(2x-7) = log39
2x-7 = 9
2x = 16
2x = 24
x = 4
K = {4}
log3( 1 + log3(2x-7)) = 1
log3( 1+ log3(2x-7)) = log33
1 + log3(2x-7) = 3
log3(2x-7) = 2
log3(2x-7) = log39
2x-7 = 9
2x = 16
2x = 24
x = 4
K = {4}
4. Solve:
log3(3x- 8) = 2 – x 3x > 8
Please log in to view the solution. 5. Solve:
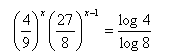
5. Solve:
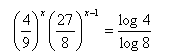
6.Solve:
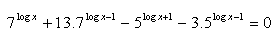
7. Solve:
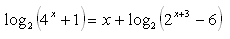
8. Solve:
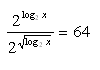
9. Solve:
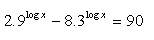
10.Solve:
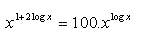
11.Solve in real numbers:
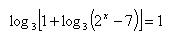
12.Solve in real numbers:
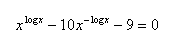
13.Solve in real numbers:
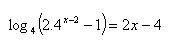
14.Solve in real numbers:
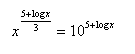
15.Solve in real numbers:
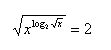
16.Solve in real numbers:
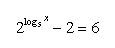
17.Solve in real numbers:
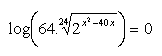
18.Solve in real numbers:
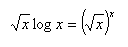
19.Solve in real numbers:
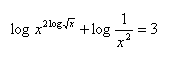
20.Solve in real numbers: