Right Triangle

1. Define a right triangle.

Solution:


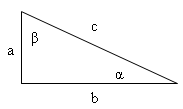
a) Pythagorean theorem:

a² + b² = c²

b) Goniometric functions:



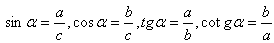
c) Perimeter:

O = a + b + c

d) Area:



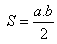
c) Euclid theorems:

a² = c.c_a
b² = c.c_b
v² = c_a.c_b

2. The catheti of a right triangle ΔABC are a =3 cm, b = 4 cm.

Solution:


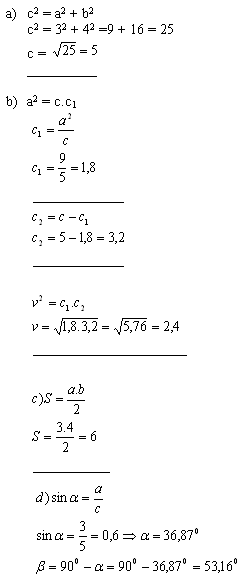
For the triangle ΔABC stands: c = 5cm, v_c = 2,4cm, S = 6cm², α = 36,87°, β = 53,16°.

3. Let a, b be a right triangles‘ catheti, c a right triangles‘ hypotenuse, α the angle opposite to a.

Fill the table! (Lengths in cm)

Solution:

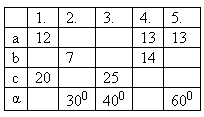
4.The sides of a right triangle make an arithmetic progression. Determine:

5.Sum of the lengths of the catheti of a right triangle is 30 cm. The area of the triangle is 110,5 cm². Determine the perimeter of the triangle.

6. The leg of an isosceles triangle is 1 cm longer than it‘s base. The altitude is 2 cm shorter than the leg. Determine the size of the leg of the triangle.

7. A triangle‘s sides lengths equal a = 4p2- 1, b = 4p, c = 4p2+1. Prove that it‘s a right triangle and that it‘s a Pythagorean triangle. Write out four Pythagorean triangles.

8. What is the gradient of the road if the traffic sign indicating it says 6,7%? The car traveled 2,3 km along this road.

9. Calculate the area of an isosceles right triangle whose perimeter is 20 cm.

10. For the legs of a right triangle, a:b = 2:3. The hypotenuse has a length of 10 cm.

Register and unlock all the solutions!

You will find a lot of exercises, sample solutions and useful materials on priklady.eu.
Registered users can see all the content – without restrictions!
Just log in and start learning effectively.

Register now and start learning!

Already have an account? Log in