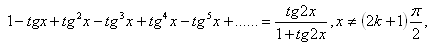Geometric Progression
1.Characterize a geometric progression:
Solution:
A progression (an)∞n=1 is told to be geometric if and only if exists such q є R real number; q ≠ 1, that for each n є N stands an+1 = an.q. Number q is called a geometric progression ratio.
Properties:
a) an = a1.qn-1
b) ar = as.qr-s
c) 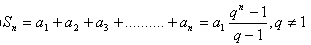
d) Stable incrementation: 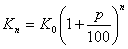
e) Stable decrementation: 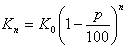
f) Sum of an infinite geometric progression: 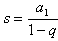 q < 1
q < 1
2.Determine first 6 members of a geometric progression if stands a3 = 8 and a7 = 128.
Solution:
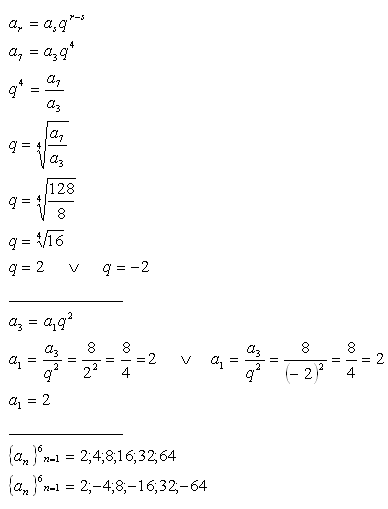
3.If a number is added to 2, 16 and 58, it results in first 3 geometric progression members. Find out the number and enumerate first 6 members of the progression.
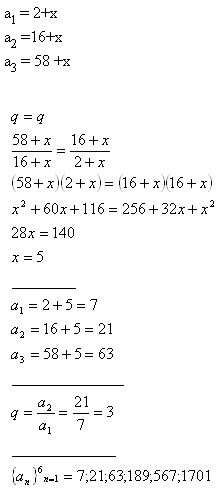
4.Insert 4 numbers between the roots of the equation x2 -66x +128 = 0 so that they would make a geometric progression.
Please log in to view the solution.5.Enumerate first 6 progression members of a geometric progression that fits following conditions:
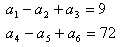
6.The surface area of a cuboid equals S = 78 cm2. The sides of the cuboid make a geometric progression. Sum of the lengths of the sides intersecting in one of the edges is 13 cm. Determine the volume of the cuboid.
Please log in to view the solution.7.An equestrian wants to buy a horse for $10,000. He made a deal with the salesman to pay for the nails in the horseshoes. He paid 1 cent for the first nail, 2 cents for the second nail, 4 cents for the third nail and so on. Each horseshoe is fastened by 5 nails. Did he make a good deal?
Please log in to view the solution.8.A workman agreed to work under following conditions: His salary for the first day of work will be $1, for the second day of work $2, for the third day of work $4, and so on. How long does he have to work to earn $4095?
Please log in to view the solution.9.What should be the bank interest to raise the deposit of $10000 to $25 000 in 5 years?
Please log in to view the solution.10.What is the sum of following infinite geometric progression?
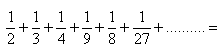
11. Solve in real numbers:
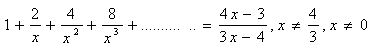
12. Solve in real numbers: