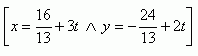Straight line and conic section
1. What do you know about the mutual position of a line and a conic section?
Solution:
The mutual position of a line and a conic section is determined by solving their system of equations, which leads to solving a quadratic equation. If
D > 0 the line is a secant
D = 0 the line is a tangent
D < 0 the line is not a secant
If the point T[ xT; yT] is the point of tangency lying on both the conic section and the line, then:
Equations of tangents:

2. Determine the mutual position of the line 2x + y – 8 = 0 and the parabola x2 + 8y = 0
Solution:

The line is a tangent It touches the parabola
3. Determine the mutual position of the line x + y – 10 = 0 and the ellipse x2 + 3y2 – 3 = 0
Solution:

A straight line is a non-intersecting line.
4. Examine the mutual position of the circle k: x2 + y2 -25 = 0 and the line p:
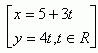
5. Determine c so that the line x – y + c = 0 is a tangent to the parabola y2 = 6x
Please log in to view the solution.6. Determine k so that the line y = kx + 3 is tangent to the hyperbola 16x2 – 25y2 - 400 = 0
Please log in to view the solution.7. Write the equations of the tangents to the circle x2 + y2 = 25 at its point of tangency T [3;y]. Also determine the angle φ between the tangents.
Please log in to view the solution.8. Write the equation of the tangent to the parabola y2 = 18x, which is parallel to the line p : 3x – 4y + 69 = 0
Please log in to view the solution.9. Determine the length of the chords cut by the circle on the coordinate axes, if the equation of the circle is x2 + y2 – 8x + 7y +12 = 0
Please log in to view the solution.10. Which tangent of the ellipse E: x2 + 4y2 -16 = 0 is parallel to the line p: