Acoustics

1.What is acoustics?

Solution:

Acoustics is the branch of physics that deals with physical phenomena involved in the transmission of sound. A source of sound is any body that can vibrate.

Sound:
a) Tone – a regular sinusoidal waveform (human vocal cords, strings, air columns, musical instruments)
b) Noise – an irregular waveform (banging, rustling, creaking)

Sound intensity:

I=PS=Wt⋅S,[I]=W m−2I=\frac{P}{S}=\frac{W}{t\cdot S},\qquad [I]=\mathrm{W\,m^{-2}}

Threshold of hearing I0=10−12 W m−2, threshold of pain Ib=10 W m−2

Sound intensity level:

L=10⋅log⁡ ⁣(II0),[L]=dB (decibel)L = 10 \cdot \log\!\left(\frac{I}{I_0}\right),\qquad [L]=\mathrm{dB}\ \text{(decibel)}

Pitch – determined by the frequency of vibration

fz=v2lf_z=\frac{v}{2l}

Timbre (tone color) – determined by the presence of higher harmonic frequencies

fk=k⋅v2lf_k = k\cdot \frac{v}{2l}

Speed of sound in air:

v=(331.8+0.61 t) m s−1v = (331.8 + 0.61\,t)\ \mathrm{m\,s^{-1}}

(where t tis temperature in °C)

String:

l=kλ2  (k=1,2,3,…),fz=v2ll = k\frac{\lambda}{2}\ \ (k=1,2,3,\ldots), \qquad f_z=\frac{v}{2l}

Open pipe:

l=kλ2  (k=1,2,3,…),fz=v2ll = k\frac{\lambda}{2}\ \ (k=1,2,3,\ldots), \qquad f_z=\frac{v}{2l}

Closed pipe:

l=kλ4  (k=1,3,5,…),fz=v4ll = k\frac{\lambda}{4}\ \ (k=1,3,5,\ldots), \qquad f_z=\frac{v}{4l

  

2.Calculate the speed of sound in air

  • a.) at temperature t = 0o C
  • b.) at temperature t = 15o C
  • c.) at what temperature is the speed of sound in air v = 351.32 m·s-1? The speed of sound in air as a function of ambient temperature is given by v = 331.8 + 0.61·t  (m·s-1).

Solution:

a.) t = 0oC, v0 = (331,8 + 0,61·0) m·s-1 = 331,8 m·s-1 => v0 = 331,8 m·s-1

b.) t = 15oC, v15 = (331,8 + 0,61·15oC) m·s-1 = 340 m·s-1 => v15 = 340 m·s-1

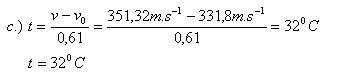
fyzika-akustika-2.gif 

The speeds of sound in air are v0 = 331,8 m·s-1, v15 = 340 m·s-1.

The speed of sound in air v = 351,32 m·s-1 is reached at temperature t = 32oC.

The speed of sound in air v15 = 340 m·s-1 is used when solving problems (unless stated otherwise).

3.Calculate the wavelengths corresponding to the limits of the audible frequency range 16 Hz – 20,000 Hz. v = 340 m·s-1.

Solution:

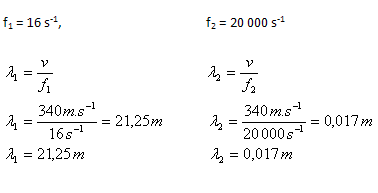
fyzika-akustika-3.gif 

The wavelengths corresponding to the limits of audibility are 0.017 m – 21.25 m.

4.Four sea ...

  • a.) On the sea surface there are two boats at a mutual distance of 11.6 km. The first sends a sound signal through the water and simultaneously a light signal above the water. The second boat receives both signals, the sound one 8 s later than the light. Determine the speed of sound in seawater.
  • b.) A sailor on a boat heard thunder 10 s after he saw the flash. At what distance did the lightning strike?
  • c.) Sound reflected from a pod of whales returned to the boat after 1 second. How far are the whales from the boat?
  • d.) On one boat the sea depth was measured with ultrasound. What is the depth there if the reflected ultrasonic signal returned to the boat after 0.8 s?
Please log in to view the solution.

5.An observer standing at the edge of the Macocha Abyss dropped a stone into it and heard it hit the bottom after 5.6 s. Determine the depth of the abyss!

t1 – time of the stone’s fall,  t2 – time of sound propagation after the impact at the bottom
Please log in to view the solution.

6.If we shorten the length of a string (with unchanged tension) by 10 cm, its fundamental frequency changes by a factor of 1.5. Determine the original length of the string l.

Please log in to view the solution.

7. What length must

  • a.) an open pipe have
  • b.) a closed pipe have
if they produce a tone with frequency f = 130.5 Hz at temperature t = –5oC?
Please log in to view the solution.

8.By how many decibels does the sound intensity level increase if the sound intensity increases 100,000 times? What will this increased intensity be?

Please log in to view the solution.

9.What is the Doppler principle (effect)?

Please log in to view the solution.

10.
John is standing by a highway along which an ambulance is moving at speed w = 20 m·s-1. The siren of the ambulance emits a steady tone of frequency 1,000 Hz. What frequency does John register when the ambulance

  • a.) is approaching
  • b.) is receding. 
The air temperature is t = 20oC
Please log in to view the solution.