Waves

1. What is a mechanical wave?

Solution:

Mechanical wave motion is a physical phenomenon in which a mechanical oscillating motion propagates through an elastic medium. In wave motion, oscillatory motion and energy are transmitted through the medium.
Wave motion can be:

a.) Transverse wave – the instantaneous displacements are perpendicular to the direction of wave propagation

  • characterized by up-and-down motion

b.) Longitudinal wave – the instantaneous displacements are in the direction of wave propagation

  • characterized by compression and rarefaction of the medium

Phase velocity v – velocity at which the wave propagates through the medium

Wavelength

  • distance the wave travels in time TT

  • distance between two nearest points oscillating in the same phase

  • distance between two nearest maxima (or minima)

  • distance between two nearest compressions (or rarefactions)

λ=v⋅T=vf\lambda = v \cdot T = \frac{v}{f}

Equation of a traveling wave:

y=ymsin⁡[2π(tT−xλ)]y = y_m \sin \left[ 2\pi \left(\frac{t}{T} - \frac{x}{\lambda}\right) \right]

The equation of a traveling wave expresses the instantaneous displacement of the wave at any given time tt and position xx.

Wave interference – the superposition of two or more waves

Phase difference:

Δφ=2πλ(x2−x1)=2πλd=ωv⋅d\Delta \varphi = \frac{2 \pi}{\lambda} (x_2 - x_1) = \frac{2 \pi}{\lambda} d = \frac{\omega}{v} \cdot d

Interference maximum:

d=2k⋅λ2,(k=0,1,2,3,… )d = 2k \cdot \frac{\lambda}{2}, \quad (k = 0, 1, 2, 3, \dots)

Interference minimum:

d=(2k+1)⋅λ2,(k=0,1,2,3,… )d = (2k + 1) \cdot \frac{\lambda}{2}, \quad (k = 0, 1, 2, 3, \dots)

 

2.The frequency range of human speech is 200 Hz to 1.5 kHz. Determine the smallest and largest wavelength of the corresponding sound wave! The speed of sound in air is about 340 m.s-1.

Solution:

Analysis:

f1 = 200 s-1, f2 = 1500 s-1, v = 340 m.s-1.

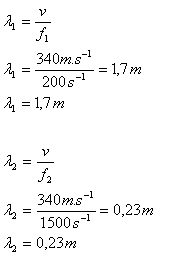
 physics-wave-2.gif

The wavelength range of human speech is from 0.23 m to 1.7 m.

3.A wave with period T = 2 ms and wavelength λ = 2.9 m propagates in water from a sound source. What is the speed of sound in water?

Solution:

Analysis:

T = 2 ms = 0.002s, λ = 2.9 m, v = ?

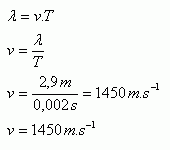
physics-wave-3.gif 

The speed of sound in water is v = 1450 m.s-1.

4.A progressive wave propagates in an elastic string according to the equation:

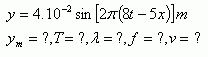
physics-wave-4-q.gif
Please log in to view the solution.

5.A wave with period T propagates along the x-axis. At coordinate x = 4 cm, at time t = T/6, the instantaneous displacement is y = 0.5ym. Determine the wavelength λ!

Please log in to view the solution.

6.A wave with period T and wavelength λ propagates from a source along a line. At time t = T/2, a point located at distance x = λ/3 from the source has instantaneous displacement y = 5 cm. Determine the amplitude ym!

Please log in to view the solution.

7.A wave with frequency 440 Hz propagates with phase velocity 340 m.s-1. Calculate the phase difference of oscillations between two points x1 and x2 located along a line through the source of the wave, with mutual distance 17 cm.

Please log in to view the solution.

8.A wave propagates along a line from a source oscillating with period T = 10-3s. Two points of this line, located at x1 = 12 m and x2 = 14.7 m from the source, oscillate with phase difference 1.5π. Determine the phase velocity of the wave!

Please log in to view the solution.