Astrofyzika
1.Ako sa v astrofyzike určujú vzdialenosti, hmotnosť a jasnosť hviezd?
Riešenie:

2.Ako sa získavajú informácie o hviezdach a vesmíre?
Charakterizujte:
- Wienov posuvný zákon
- Štefan – Boltzmanov zákon
- Žiarivý tok
- Žiarivý výkon
- Charakteristiky Slnka
- Rozpínanie vesmíru
- Dopplerov zákon
- Hublerov zákon
Riešenie:

3.Vypočítajte za aký čas prejde svetlo vo vákuu vzdialenosť rovnajúca sa
- a) priemeru slnečnej sústavy (s = 80 AU)
- b) priemeru galaxie (s = 30 kpc)
Riešenie:
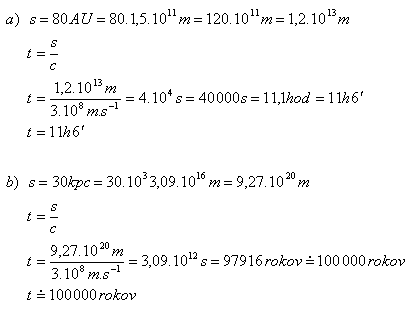
Svetlo prejde priemer slnečnej sústavy za 11 hodín, priemer galaxie za asi 100 000 rokov.
4.Vypočítajte strednú hustotu látky v Slnečnej sústave. Predpokladáme, že všetku hmotnosť sústavy vytvára Slnko (Mo = 2.1030kg )a že Slnečná sústava je guľa s polomerom R = 40 AU.
Prihláste sa pre zobrazenie riešenia
5.Slnko obieha okolo stredu Galaxie rýchlosťou v = 250 km.s-1, približne po kružnici s polomerom r=10 kpc. Určite obežnú dobu Slnka. Akou veľkou gravitačnou silou je Slnko priťahované k stredu Galaxie?
Prihláste sa pre zobrazenie riešenia
6.Uvažujme o guľovej hviezdokope s hmotnosťou MHK = 2.105Mo, ktorá obieha okolo stredu Galaxie (MG=1,4.1011Mo) po kružnici s polomerom r=12 kpc. Určite:
- a) silu, ktorou je hviezdokopa priťahovaná k stredu Galaxie
- b) dostredivé zrýchlenie hviezdokopy
- c) rýchlosť hviezdokopy vzhľadom na stred Galaxie
7. Odvoďte vzorec pre výpočet hmotnosti hviezdy (planéty) pomocou jej obežnice.
Prihláste sa pre zobrazenie riešenia
8.Vypočítajte hmotnosť planéty Mars pomocou mesiaca Deimos, ktorý obieha okolo Marsa po kružnici s polomerom r = 23,5.106m, s obežným časom 1,26dňa (pozemského)
Prihláste sa pre zobrazenie riešenia
9.Druhý Jupiterov mesiac Európa obieha okolo Jupitera po kružnici s polomerom r1 = 6,71.108m a s obežnou dobou T = 3,88 dňa. Vypočítajte, koľkokrát je hmotnosť Jupitera väčšia, ako hmotnosť Zeme.
Prihláste sa pre zobrazenie riešenia
10.Súčet hmotností zložiek dvojhviezdy je 3,5Mo, zložky obiehajú okolo spoločného ťažiska s periódou T = 320 rokov. Určite vzájomnú polohu zložiek kolmú na smer zorného lúča, ktorú by sme videli pod uhlom π = 3,1//a vzdialenosť dvojhviezdy od Slnka.
Prihláste sa pre zobrazenie riešenia
11.Zdanlivá hviezdna magnitúda Slnka je -26,8m. Vypočítajte jeho absolútnu magnitúdu M.
Prihláste sa pre zobrazenie riešenia
12.Do akej vzdialenosti možno pri meraní vzdialenosti galaxií využiť supernovy, ktorá v nich zažiarila, ak jej maximálna absolútna magnitúda je –16M a ak máme ďalekohľad ktorým pozorujeme hviezdy do zdanlivej hviezdnej magnitúdy +22m?
Prihláste sa pre zobrazenie riešenia
13.Akú paralaxu π má hviezda, ak rozdiel zdanlivej a absolútnej hviezdnej magnitúdy je +8
Prihláste sa pre zobrazenie riešenia
14.Aká je vlnová dĺžka, na ktorú pripadá maximum vyžarovania a intenzita vyžarovania hviezdy, ktorá má teplotu 30 000K?
Prihláste sa pre zobrazenie riešenia
15.Červený obor má povrchovú teplotu 3500K, polomer R = 36.Ro, hmotnosť M = 3,6 Mo. Vypočítajte jeho priemernú hustotu ρ a žiarivý výkon L. (σ = 5,67.10-8W.m-2.K–4)
Prihláste sa pre zobrazenie riešenia
16.Vypočítajte polomer a priemernú hustotu bieleho trpaslíka, ktorého hmotnosť M = 2,35Mo, povrchová teplota T = 12 500K, žiarivý výkon L = 0,0036 Lo. Ro = 6,96.108m, T0 = 5780K
Prihláste sa pre zobrazenie riešenia
17.Aký žiarivý tok dopadá zo Slnka na plochu s obsahom S = 1m2 (Žiarivý výkon Slnka je L=3,83.1026W)
- na Venušu (r = 0,72AU)
- na Jupiter (r = 5,2AU)
18.Hviezda má zdanlivú magnitúdu m1=4. Aká by bola zdanlivá magnitúda m2 tejto hviezdy, keby bola v dvojnásobnej vzdialenosti od nás?
Prihláste sa pre zobrazenie riešenia
19.Uvažujme o vzdialenej galaxii, ktorá sa od našej Galaxie vzďaľuje rýchlosťou v=6000 km.s-1. Akú vlnovú dĺžku spektrálnej čiary vodíka odmeriame, ak jej pôvodná vlnová dĺžka je 656,3 nm? V akej vzdialenosti od nás sa táto galaxia pravdepodobne nachádza?
Prihláste sa pre zobrazenie riešenia20.Určite čas za ktorý sa náš vesmír rozpína. Určite čas, ktorý uplynul od „veľkého tresku“ po súčasnosť.
Prihláste sa pre zobrazenie riešenia