Fyzikálny význam derivácie
1. V čom spočíva fyzikálny význam derivácie?
Riešenie:
- Okamžitá rýchlosť v čase t0 je prvou deriváciou dráhy podľa času:
v(t0) = s‘(t0).
- Okamžité zrýchlenie v čase t0 je prvou deriváciou rýchlosti podľa času:
a(t0) = v‘(t0)
Príklad:
Určite okamžitú rýchlosť a okamžité zrýchlenie pohybu v čase t, ktorého dráha je daná vzťahom : 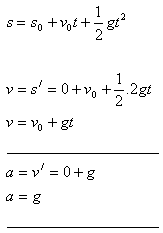
2.Kameň vyhodený z výšky h=10m kolmo nahor má počiatočnú rýchlosť v0=20m.s-1. Akú rýchlosť bude mať kameň v čase t=1,5s? Za aký čas dosiahne maximálnu výšku? Akú výšku dosiahne? (g = 10m.s-2)
Riešenie:
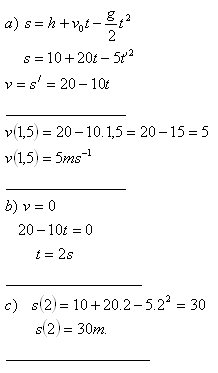
Rýchlosť kameňa v čase t = 1,5s je v = 5ms-1. Maximálnu výšku 30m dosiahne za 2 sekundy.
3.Teleso zíde po naklonenej rovine 50m dlhej za 10s. Aká je jeho konečná rýchlosť,ak predpokladáme, že dráha je kvadratická funkcia času a že začiatočná rýchlosť je nulová.
Riešenie:
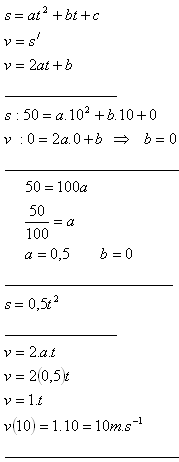
Konečná rýchlosť telesa je v = 10m.s-1
4.Rýchlik idúci rýchlosťou 90km.h-1 má zabrzdiť tak, aby sa rovnomerne spomaleným pohybom zastavil na vzdialenosti 1km. Po akom čase zastaví?
5.Zistite ako rýchle sa mení výška s tlakom vzduchu .
Vzorec, ktorý udáva výšku nad zemským povrchom v závislosti od tlaku vzduchu. (p0 – je normálny tlak vzduchu na hladine mora):
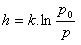
6.Určite rýchlosť zmeny napätia (p) vodných pár od absolútnej teploty (T), ak platí:
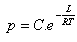
(C,L,R sú konštanty)
7.Množstvo elektrického náboja Q , ktorý prechádza vodičom sa mení s časom podľa vzťahu Q = 3t2 +2t +2 . ( [Q] = C, [t] = sec )
8.V indukčnej cievke preteká prúd i = 15.sin5(3t), [i] = A, [t] = sec, [L = 0,03 H] Vypočítajte indukované elektromotorické napätie v čase t = 2π/9 sec. podľa vzťahu:
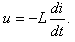
9.Teleso sa pohybuje po priamke a pre jeho výchylku z rovnovážnej polohy platí : y = 2cos2πt - 3sin2πt. Nájdite jeho rýchlosť v čase t = 1s a najväčšiu výchylku z rovnovážnej polohy. (y je v cm)
Prihláste sa pre zobrazenie riešenia
10.Výkon batérie s elektromotorickou silou E a vnútorným odporom Ri je : P = E.I – Ri.I2. Pri akom prúde dá batéria najväčší výkon? Určite tento výkon.
Prihláste sa pre zobrazenie riešenia
11.Pre výpočet dráhy harmonického pohybu platí s = A.sin(ω.t). Odvoďte vzťah pre výpočet rýchlosti a zrýchlenia harmonického pohybu.
Prihláste sa pre zobrazenie riešenia
12.Závislosť medzi množstvom a hmotnosťou pri niektorých chemických reakciách je daná rovnicou
x = A.(1 – e–kt). (A, k sú konštanty).
13. Zotrvačník sa otáča, je pribrzdený a začne sa pohybovať podľa rovnice
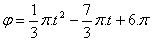
Napíšte rovnicu uhlovej rýchlosti a zistite za aký čas prejde pohyb v rovnomerný otáčavý s uhlovou
rýchlosťou ω = π .
14.Pohyb piesta tam a späť závisí od času podľa rovnice s = –1,5t3 + 9t2 (cm). Vypočítajte maximálnu vzdialenosť, ktorú piest dosiahne za 4 sekundy. Určite tiež rýchlosti v0, v1,........v6.
Prihláste sa pre zobrazenie riešenia
15.Pri pohybe telesa je dráha popísaná rovnicou s = t2 + 3t – 5 (m) pričom v čase t = 0 sec. bola jeho rýchlosť nulová. Určite dráhu, rýchlosť a zrýchlenie v čase t = 5s. Určite tiež jeho kinetickú energiu, ak jeho hmotnosť je 8kg.
Prihláste sa pre zobrazenie riešenia
16.Teleso sa pohybuje po dráhe s = t2 – t3/3 + 3t + 8 (m). Vypočítajte
- a.) za aký čas zastaví
- b.) aké bude jeho zrýchlenie v čase t = 0,5s
- c.) akú dráhu prejde teleso do zastavenia
17.Množstvo elektrického náboja, ktorý prechádza vodičom sa men podľa vzťahu Q = 2.t.e–t. Zistite čas, kedy sa intenzita prúdu bude rovnať nule.
Prihláste sa pre zobrazenie riešenia
18.Presvedčte sa, že daná funkcia opisujúca priebeh elektrického prúdu vybíjajúceho sa kondenzátora, vyhovuje diferenciálnej rovnici:
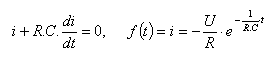
Prihláste sa pre zobrazenie riešenia