Hydrostatika
1.Zopakujme si základné vlastnosti „ideálnej kvapaliny“.
Riešenie:
Ideálna kvapalina je model kvapaliny s týmito vlastnosťami:
- a) nemá viskozitu, je dokonale tekutá
- b) je kontinuum – neuvažujeme jej časticovú štruktúru
- c) je nestlačiteľná
Stav kvapaliny v určitom jej bode určuje tlak p:
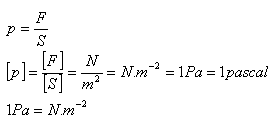
Tlak vyvolaný vonkajšou silou – Pascalov zákon:
Tlak vyvolaný vonkajšou silou pôsobiacou na povrch kvapaliny je vo všetkých miestach kvapaliny rovnaký.
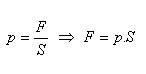
Tlak spôsobený tiažou kvapaliny – hydrostatický tlak
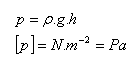
ρ – hustota kvapaliny, g = 10m.s-2, h – hĺbka, vzdialenosť od povrchu
Hydraulický princíp:
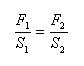
Archimedov zákon:
Teleso ponorené do kvapaliny je nadľahčované hydrostatickou vztlakovou silou, ktorá sa rovná tiaži kvapaliny telesom vytlačenej.
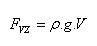
ρ – hustota kvapaliny,
V – objem ponorenej časti telesa
objem vytlačenej kvapaliny
2.Na piest s priemerom d = 20 cm, ktorý je položený na povrchu kvapaliny pôsobíme silou F = 50 N. Aký veľký tlak vyvolá sila v kvapaline?
Riešenie:
Rozbor:
d = 20 cm = 0,2 m, F = 50 N, p = ?
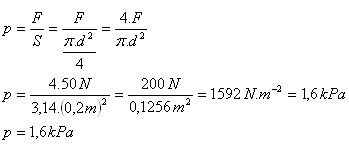
Sila vyvolá v kvapaline tlak asi 1,6 kPa.
3.Vypočítajte tlak morskej vody (ρ = 1025 kg.m-3) na dno mora
- a.) v hĺbke 3,6 km pod hladinou
- b.) v najhlbšej morskej priepasti tzv. Mariánskej priekope v Tichom oceáne (h = 11034 m)
Riešenie:
- a.) p = ρ.g.h =1025 kg.m-3.10m.s-2.3600m =36 900 000 Pa = 36,9 MPa
- b.) p = ρ.g.h = 1025 kg.s-2.10 m.s-2.11034m = 113098500 Pa = 113,1 MPa
V hĺbke 3,6 km je tlak morskej vody 36,9 MPa, na dne Mariánskej priekopy je tlak morskej vody 113,1 MPa.
4.Ľudia sú počas celého života zvyknutí na tlak vzduchu okolo 1013 h Pa. Do akej hĺbky sa môžu ponoriť do morskej vody (ρ = 1025 kg.m-3) bez prístrojov?
Prihláste sa pre zobrazenie riešenia
5.Do spojených nádob tvaru U bola naliata voda (ρ1 = 1000 kg.m-3) a ortuť. Voda v jednom rameni siahala do výšky h1 = 100 cm, ortuť v druhom rameni do výšky h2 = 7,35 cm. Určite hustotu ortute ρ2
Prihláste sa pre zobrazenie riešenia
6.Vo valcovej nádobe s podstavou S = 100 cm2 sú 2 kg ortuti (ρ1 = 13 600 kg.m-3) a 1 kg vody (ρ2 = 1000 kg.m-3). Určite hydrostatický tlak na dno nádoby!
Prihláste sa pre zobrazenie riešenia
7.Vypočítajte tlakovú silu pôsobiacu na viečko zaváraninovej fľaše s priemerom 8 cm, ak vnútorný tlak pary je 2,5 kPa a atmosférický tlak je 101325 Pa. (Predpokladáme, že vzduch vo vnútri fľaše je celkom vyčerpaný).
Prihláste sa pre zobrazenie riešenia
8.Turista nameral na úpätí hory atmosférický tlak 1020 hPa, na vrchole hory tlak 955 hPa. Aký výškový rozdiel turista pri výstupe na horu prekonal? (ρvzduch = 1,3 kg.m-3)
Prihláste sa pre zobrazenie riešenia
9.Malý hydraulický lis má priemer piesta 1,4 m, priemer piesta pumpy je 8 cm. Aká veľká sila pôsobí na piest lisu, ak na piest pumpy pôsobí sila 4 N?
Prihláste sa pre zobrazenie riešenia
10.Polomer kruhovej podstavy menšieho piesta hydraulického lisu je 4 cm. Aký polomer musí mať kruhová podstava druhého väčšieho piesta, ak silou 80 N treba vyvolať tlakovú silu 11 520 N.
Prihláste sa pre zobrazenie riešenia
11.Norma udáva, že v ponorke pre jedného námorníka musí byť priemerne 20 m3 priestoru. Koľko námorníkov môže pracovať v ponorke, ak pri ponorení do morskej vody (ρ = 1020 kg.m-3) pôsobí na povrch ponorky vztlaková sila 15,3 MN.
Prihláste sa pre zobrazenie riešenia
12.Drevený klát plávajúci na vode (ρ = 1000 kg.m-3) má ponorené dve tretiny svojho objemu. Aká je hustota dreva?
Prihláste sa pre zobrazenie riešenia
13. Hustota morskej vody je 1030 kg.m-3, hustota ľadu je 915 kg.m-3. Koľko percent ľadovca vyčnieva nad voľnou hladinou mora?
Prihláste sa pre zobrazenie riešenia
14.Aký plošný obsah musí mať ľadová kryha (tvaru kvádra) hrúbky 30 cm, ktorá unesie človeka s batožinou o celkovej hmotnosti 96 kg.
Prihláste sa pre zobrazenie riešenia15.Balón tvaru gule je naplnený vodíkom (ρ1 = 0,09 kg.m-3). Aký musí byť polomer balóna, aby mohol niesť záťaž 350 kg. Hustota vzduchu je ρ = 1,3 kg.m-3.
Prihláste sa pre zobrazenie riešenia
16. Vysvetlite ako sa vážením telesa vo vzduchu a v kvapaline (vo vode) dá zistiť hustota telesa.
- ρ – hustota kvapaliny
- ρ1- hľadaná hustota telesa
- Fg – tiaž telesa vo vzduchu (váženie telesa vo vzduchu)
- F - tiaž telesa v kvapaline (váženie telesa v kvapaline)
- FVZ – ρ.g.V (FVZ < Fg)
17.Vysvetlite, ako Archimédes (287 – 212 pred n.l.) zisťoval, či kráľovská koruna gréckeho kráľa Hierona je z čistého zlata. (ρ1 = 19 290 kg.m-3). Akú odpoveď dal kráľovi?
Prihláste sa pre zobrazenie riešenia18.Skúmavka s rovnakým prierezom zaťažená brokmi sa ponorí do vody do hĺbky 18 cm, v zriedenej kyseline sírovej do hĺbky 16 cm. Určite hustotu zriedenej kyseliny sírovej.
Prihláste sa pre zobrazenie riešenia
19. Oceľová guľa (ρ1 = 7800 kg.m-3) je zavesená na vlákne a ponorená do vody (ρ = 1000 kg.m-3). Objem gule je V = 1 dm3. Akou silou je napínané vlákno?
Prihláste sa pre zobrazenie riešenia
20.Guľôčku zvážime vo vzduchu i vo vode. Získané hodnoty sú Fg = 1,4 N, F = 0,84 N. Hustota vody: ρ = 1000 kg.m-3.
- a.) Z akého materiálu je guľôčka?
- b.) Aký je jej polomer
21.Aká je hustota kameňa s hmotnosťou 12,6 kg, ak na jeho vytiahnutie z vody je potrebná sila, ktorej veľkosť je 81,2 N? Hustota vody je 996,8 kg.m-3.
Prihláste sa pre zobrazenie riešenia