Extrémy – slovné úlohy
1.Číslo 32 rozložte na dvoch sčítancov tak, aby ich súčin bol najväčší.
Riešenie:
Prvý sčítanec : x x = 16
Druhý sčítanec : 32 – x 32 – 16=16
y = x.(32 – x)
y = 32x – x2
y‘ = 32 – 2x
32 – 2x = 0
2x = 32
x =16
y‘‘ = -2 < 0 - maximum
Prvý sčítanec je 16, druhý tiež 16
2.Číslo 16 rozložte na dvoch sčítancov tak, aby súčet druhých mocnín týchto sčítancov bol najmenší.
Riešenie:
Prvý sčítanec : x x = 8
Druhý sčítanec : 16 – x 16 – 8 = 8
y = x2 + ( 16 – x )2
y = x2 + 256 -32x +x2
y = 2x2 – 32x + 256
y‘ = 4x – 32
4x - 32 = 0
4x = 32
x = 8
y‘‘ = 4 > 0 - minimum
Prvý sčítanec je 8, druhý tiež 8.
3.Nájdite také kladné číslo x, aby súčet tohto čísla a jeho prevrátenej hodnoty bol najmenší.
Riešenie:
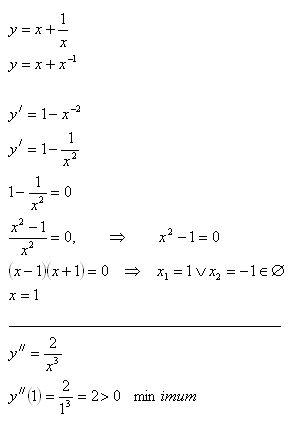
Hľadané číslo je x = 1.
4.Z drôtu dĺžky l = 120 cm máme urobiť model kvádra so štvorcovou podstavou. Aké má mať rozmery, aby povrch bol maximálny?
Prihláste sa pre zobrazenie riešenia
5. Záhrada tvaru obdĺžnika má obvod 200 m. Určite rozmery záhrady tak, aby jej obsah bol maximálny.
Prihláste sa pre zobrazenie riešenia
6.Kedy má kváder s objemom V = 63 cm3 a výškou v = 7 cm najmenší povrch?
Prihláste sa pre zobrazenie riešenia
7.Na brehu rieky treba oplotiť záhradu obdĺžnikového tvaru (jednu stranu obdĺžnika tvorí rieka) pletivom dlhým l = 800 m. Aké rozmery musí mať záhrada , aby jej výmera bola maximálna ?
Prihláste sa pre zobrazenie riešenia
8.Aké sú rozmery otvoreného bazéna so štvorcovým dnom, ak bazén má objem V = 32 m3 a ak na jeho vymurovanie sa má spotrebovať minimálne množstvo materiálu.
Prihláste sa pre zobrazenie riešenia
9. Drôt s dĺžkou 5 m ohnite do pravého uhla tak, aby vzdialenosť obidvoch koncov bola minimálna. Kde treba drôt ohnúť?
Prihláste sa pre zobrazenie riešenia
10. Z plechu tvaru štvorca so stranou 30 cm treba v rohoch vystrihnúť štyri rovnaké štvorčeky , zvyšok prehnúť tak, aby vznikla otvorená škatuľa. Určite stranu odstrihnutých štvorčekov x tak, aby objem škatule bol maxi-málny.
Prihláste sa pre zobrazenie riešenia
11.Jama s objemom 500 m3 má tvar kvádra so štvorcovou podstavou so stranou x a hĺbkou h. Pri akých rozmeroch x a h bude mať jama minimálny povrch?
Prihláste sa pre zobrazenie riešenia
12.Daná je parabola y = 4 – x2. Nájdite vrcholy obdĺžnika ABCD s najväčším obvodom, ktorého vrcholy A,B ležia na osi x , vrcholy C,D majú kladné y-ové súradnice a ležia na parabole.
Prihláste sa pre zobrazenie riešenia
13.Určite rozmery (r, v) valcovej nádoby bez veka, ktorej povrch je S = 27π tak, aby jej objem bol najväčší.
Prihláste sa pre zobrazenie riešenia
14.Hore otvorená nádoba tvaru valca má objem V = 3140 cm3. Určite rozmery valca (r, v) tak, aby na vytvorenie tejto nádoby sa minulo najmenej materiálu.
Prihláste sa pre zobrazenie riešenia
15. Aké rozmery musí mať obdĺžnik s obvodom O = 40cm, aby jeho uhlopriečka bola minimálna.
Prihláste sa pre zobrazenie riešenia