Geometrický význam derivácie
1.Aký je geometrický význam derivácie?
Riešenie:
Pomocou derivácie funkcie y = f(x) môžeme napísať rovnicu dotyčnice alebo rovnicu normály ku grafu funkcie v bode T [xT , yT]
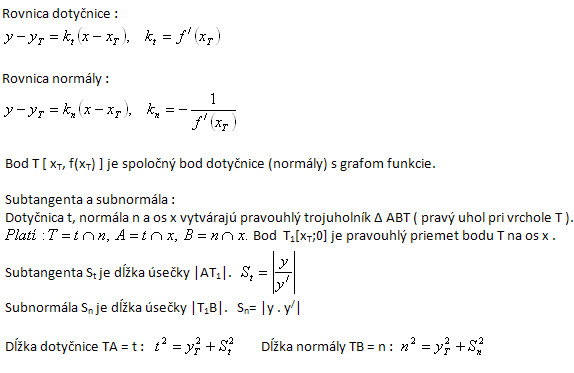
2. Napíšte rovnicu dotyčnice a rovnicu normály ku krivke:
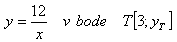
Riešenie:
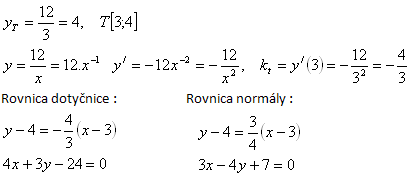
3. Napíšte rovnicu dotyčnice a rovnicu normály ku krivke:
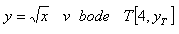
Riešenie:

4. Napíšte rovnicu dotyčnice a rovnicu normály ku krivke:
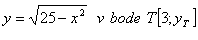
5. Napíšte rovnicu dotyčnice a rovnicu normály ku krivke:
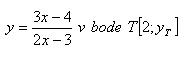
6. Napíšte rovnicu dotyčnice a rovnicu normály ku krivke y=ln(x+1) v bode T[0; yT]
Prihláste sa pre zobrazenie riešenia
7. Napíšte rovnicu dotyčnice ku krivke y = sin 2x v bode T [3π/4 ;yT].
Prihláste sa pre zobrazenie riešenia
8. Napíšte rovnicu dotyčnice ku krivke y = x2 – 4x + 3 , ktorá zviera s osou x uhol φ = 450.
Prihláste sa pre zobrazenie riešenia
9.Nájdite rovnicu dotyčnice ku krivke y = x2 -2x +3 , ak dotyčnica je rovnobežná s priamkou p : 3x -y + 5 = 0.
Prihláste sa pre zobrazenie riešenia
10. Je daná funkcia f : y = x3- 9x2 +15x +3 . Určite dotykové body vodorovných dotyčníc.
Prihláste sa pre zobrazenie riešenia
11. Určite uhol φ medzi dvoma dotyčnicami krivky ak jedna má bod dotyku T1[ 3;yT1] a druhá T2[-3; yT2]. Rovnica krivky:
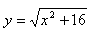
12. Určite dĺžku subtangenty, subnormály, dotyčnice a normály ku grafu funkcie v bode T[1;yT]. Funkcia má rovnicu:
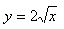
13. Vypočítajte dĺžku subtangenty, subnormály, dotyčnice a normály ku grafu funkcie y = 2x v bode T [1;yT].
Prihláste sa pre zobrazenie riešenia