Variácie
1. Definujte a charakterizujte variácie a variácie s opakovaním.
Variácie
Variácia k-tej triedy z n prvkov je každá usporiadaná k-tica rôznych prvkov, vybraných z n-prvkovej množiny. V k-tici záleží na poradí prvkov. V k-tici sa ani jeden z prvkov neopakuje.
Počet variácií:
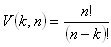
Variácie s opakovaním
Variácia k-tej triedy z n prvkov s opakovaním je každá usporiadaná k-tica prvkov vybraných z n-prvkovej množiny. V k-tici sa môžu prvky ľubovoľne opakovať.
Počet variácií s opakovaním:
V*(k,n) = nk
2. Daná je množina M = {a,b,c,d}. Z prvkov tejto množiny vytvorte variácie 2.triedy bez opakovania a s opakovaním. Vypočítajte ich počet.
a) Variácie:
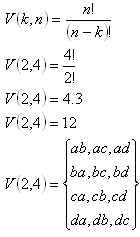
b) Variácie s opakovaním:
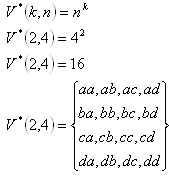
3. Do školského výboru zvolili 7 žiakov. Koľkými spôsobmi sa dá z nich vybrať predseda, podpredseda, tajomník a pokladník?
Sú to variácie: n = 7, k = 4
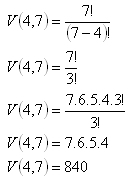
Funkcionári výboru sa dajú vybrať 840 spôsobmi.
4. Osem študentov si sľúbilo, že si z prázdninových ciest navzájom pošlú pohľadnice.
Koľko pohľadníc rozoslali?
5. Z koľkých rôznych prvkov môžeme vytvoriť 240 variácií 2.triedy?
Prihláste sa pre zobrazenie riešenia6. Ak sa počet prvkov zväčší o 2, zväčší sa počet variácií 3. triedy o 384. Koľko je prvkov?
Prihláste sa pre zobrazenie riešenia7. Vo vrecku je 6 rôznych lístkov označených číslicami 1 až 6. Koľkými rôznymi spôsobmi môžeme postupne, s prihliadnutím na poradie vybrať tri z nich, ak vybrané lístky sa do vrecka
a) nevracajú.
b) vracajú.
8. Počet variácií bez opakovania 3.triedy z x prvkov je o 225 menší než počet variácií 3.triedy s opakovaním z tých istých prvkov. Koľko je prvkov?
Prihláste sa pre zobrazenie riešenia9. Počet trojčlenných variácií bez opakovania je 10 násobkom dvojčlenných variácií bez opakovania tej istej množiny prvkov. Koľko prvkov má táto množina?
Prihláste sa pre zobrazenie riešenia
10.Hoďme troma kockami – bielou, modrou, žltou.
- a.) Koľko rôznych výsledkov môžeme dostať?
- b.) Koľko rôznych súčtov môže padnúť?
- c.) Koľkými spôsobmi môže padnúť súčet 13